• The volume of a 3D shape is the amount of fillable space on the inside.
• Volume is measured in cubic units (units ³).
• The surface area of a 3D shape is the amount of coverable space on the outside.
• Surface Area is measured in square units (units ²).

Here’s how to calculate the volume and surface area of various shapes:

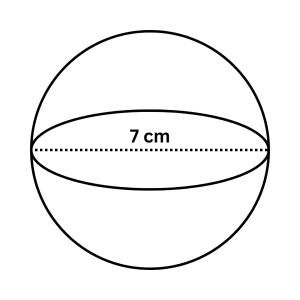
1.) Find the volume and surface area of the sphere below.

. 

VOLUME:
The formula for the volume of a sphere is:
Volume = 4/3 πr³

• r is the radius of the sphere.

In our figure, we’re given the diameter (7 cm).
To calculate the radius, just cut the diameter in half.
So, r = 3.5 cm
All we need to do now is substitute 3.5 cm into our formula.

V= 4/3 πr³
V = 4/3 π (3.5 cm)³
V = 4/3 π (42.875 cm³)
V = (4/3)(42.875)π cm³
V ≈ 57.17 π cm³ OR V ≈ 179.6 cm³

SURFACE AREA:
The formula for the surface area of a sphere is:
SA =4πr²
SA = 4π(3.5 cm)²
SA = 4π(12.25 cm²)
SA = 4(12.25)π cm²
SA = 49π cm² OR SA≈ 153.9 cm²

2.) Find the volume and surface area of the cone below.

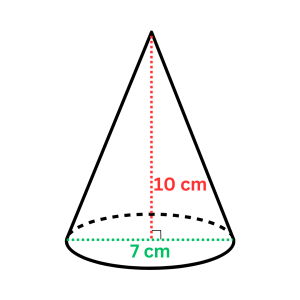
VOLUME:
The formula for the volume of a cone is:
Volume = 1/3πr²h

• r is the radius of the circular base.
• h is the height of the cone.

In our figure, we’re given the diameter (7 cm).
To calculate the radius, just cut the diameter in half.
So, r = 3.5 cm and h = 10 cm.
All we need to do now is substitute our values into our formula.

V= 1/3πr²h
V = 1/3π(3.5 cm)²(10 cm)
V = 1/3 π (3.5 cm)(3.5 cm)(10 cm)
V = 1/3 π(12.25 cm²)(10 cm)
V = 1/3 π(122.5 cm³)
V = 1/3(122.5)π cm³
V = 245/6π cm³ OR V ≈ 40.8π cm³ OR V ≈ 128.3 cm³

SURFACE AREA:
The formula for the surface area of a cone is:
SA = πr² + πrs

• r is the radius of the circular base.
• s is the slant height of the cone (the length of the slanted side).

In our figure, we’re given the diameter (7 cm).
To calculate the radius, just cut the diameter in half.
So, r = 3.5 cm.

In our figure, we’re not given the slant height, but we can find it using the Pythagorean theorem.
r² + h² = s²
(3.5 cm)² + (10 cm)² = s²
12.25 cm² + 100 cm² = s²
112.25 cm² = s²
√(112.25 cm²) = √(s²)
10.6 cm ≈ s

All we need to do now is substitute our values into our formula.

SA = πr² + πrs
SA ≈ π(3.5 cm)² + π(3.5 cm)(10.6 cm)
SA ≈ π(12.25 cm²) + π(37.1 cm²)
SA ≈ π(12.25 cm² + 37.1 cm²)
SA ≈ π(49.35 cm²)
SA ≈ 49.35π cm² OR SA ≈ 155 cm²

3.) Find the volume and surface area of the cylinder below.

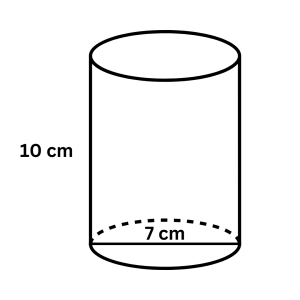
VOLUME:
The formula for the volume of a cylinder is:
Volume = πr²h

• r is the radius of the circle
• h is the height of the cylinder.

In our figure, the height is 10 cm.
We need the radius, but we’re given the diameter (7 cm).
To calculate the radius, just cut the diameter in half.
So, r = 3.5 cm
All we need to do now is substitute the values into our formula.

V= πr²h
V = π(3.5 cm)²(10 cm)
V = π(12.25 cm²)(10 cm)
V = π(122.5 cm³)
V = 122.5π cm³ OR V ≈ 384.9 cm³

SURFACE AREA:
To find the surface area of the entire figure, find the area of each face.

Note: The two bases are both circles, so we’ll use A = πr² for those.
To find the area of the side, imagine cutting straight up the side of the cylinder and laying it flat. You would end up with a rectangle.
The height of the rectangle would be 10 cm, and the length of the rectangle would be equal to the circumference of the circular base.
That means that the area of the curved side of the cylinder would be length times height, or in this case : (2πr) times height.

Area of bottom = πr² = π(3.5 cm)² = π(12.25 cm²) = 12.25π cm²
Area of the top = πr² = π(3.5 cm)² = π(12.25 cm²) = 12.25π cm²
Area of the curved side = 2πrh = 2π(3.5 cm)(10 cm) = 2π(35 cm²) = 70πcm²

Surface area = The sum of the areas of all 3 faces
SA = 12.25π cm² + 12.25π cm² + 70πcm²
SA = 24.5π cm² + 70π cm²
SA = 94.5π cm² OR SA ≈ 296.9 cm²

4.) Find the volume and surface area of the triangular prism below.

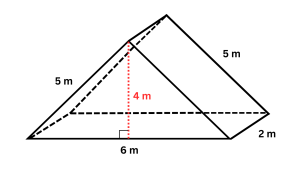
VOLUME:
The formula for the volume of a triangular prism is:
Volume = ½ b • h • d

• b is the base of a triangle
• h is the height of a triangle
• d is the distance between triangles.

In our figure: b = 6 m, h = 4 m, and d = 2 m.
All we need to do is substitute the values into our formula.

V= ½ b • h • d
V = ½ (6 m)(4 m)(2 m)
V = 3 m (4m)(2 m)
V = 12 m² (2 m)
V = 24 m³

SURFACE AREA:
To find the surface area of the entire figure, find the area of each face.
Remember: Area of a triangle is ½ b • h and area of a rectangle is b • h.

Area of bottom = 6 m • 2 m = 12 m²
Area of right side = 2 m • 5 m = 10 m²
Area of left side = 2 m • 5 m = 10 m²
Area of front triangle = ½ (6 m)(4 m) = 12 m²
Area of back triangle = ½ (6 m)(4 m) = 12 m²

Surface area = The sum of the areas of all 5 faces
SA = 12 m² + 10 m² + 10 m² + 12 m² + 12 m²
SA = 22 m² + 22 m² + 12 m²
SA = 56 m²

5.) Find the volume and surface area of the rectangular prism below.

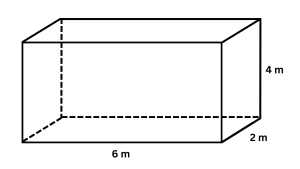
VOLUME:
The formula for the volume of a rectangular prism is:
Volume = length • width • height
In our figure, the length is 6 m, the width is 2 m, and the height is 4 m.
All we need to do is substitute the values into our formula.

V= l • w • h
V = (6 m)(2 m)(4 m)
V = (12 m²)(4m)
V = 48 m³

SURFACE AREA:
To find the surface area of the entire figure, find the area of each face.
Area of bottom = 6 m • 2 m = 12 m²
Area of top = 6 m • 2 m = 12 m²
Area of right side = 2 m • 4 m = 8 m²
Area of left side = 2 m • 4 m = 8 m²
Area of front = 6 m • 4 m = 24 m²
Area of back = 6 m • 4 m = 24 m²

Surface area = The sum of the areas of all 6 faces
SA = 12 m² + 12 m² + 8 m² + 8 m² + 24 m² + 24 m²
SA = 24 m² + 16 m² + 48 m²
SA = 88 m²