Square Root Charts
Square Root Charts
Printable square root charts are available here in a variety of fun, designed themes and ranges to support math learning at different levels. We offer charts for square roots 1-30 (typically introduced in elementary/early middle school), 1-50 (a common range for middle school students), and 1-100 (used in middle school, high school, and beyond). All charts are in easy-to-print PDF format. These resources are perfect for classroom use, homework assistance, or at-home reinforcement. Find the perfect printable chart to complement your math lessons. They can be used for:
- Memorization: Repeated exposure to the charts can help students memorize common square roots.
- Homework Help: The charts provide a quick reference for checking answers and understanding concepts.
- Classroom Activities: Teachers can use the charts for various activities, such as quizzes, games, and problem-solving exercises.
- Test Preparation: The charts can be a valuable tool for reviewing square roots before tests.
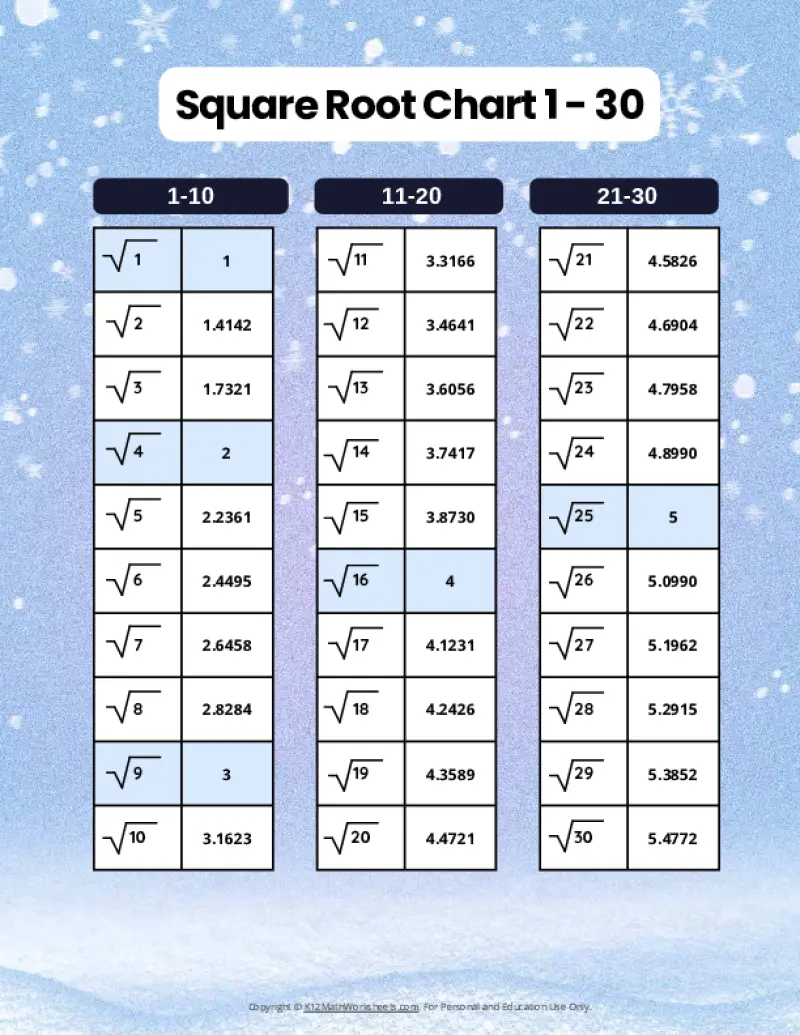
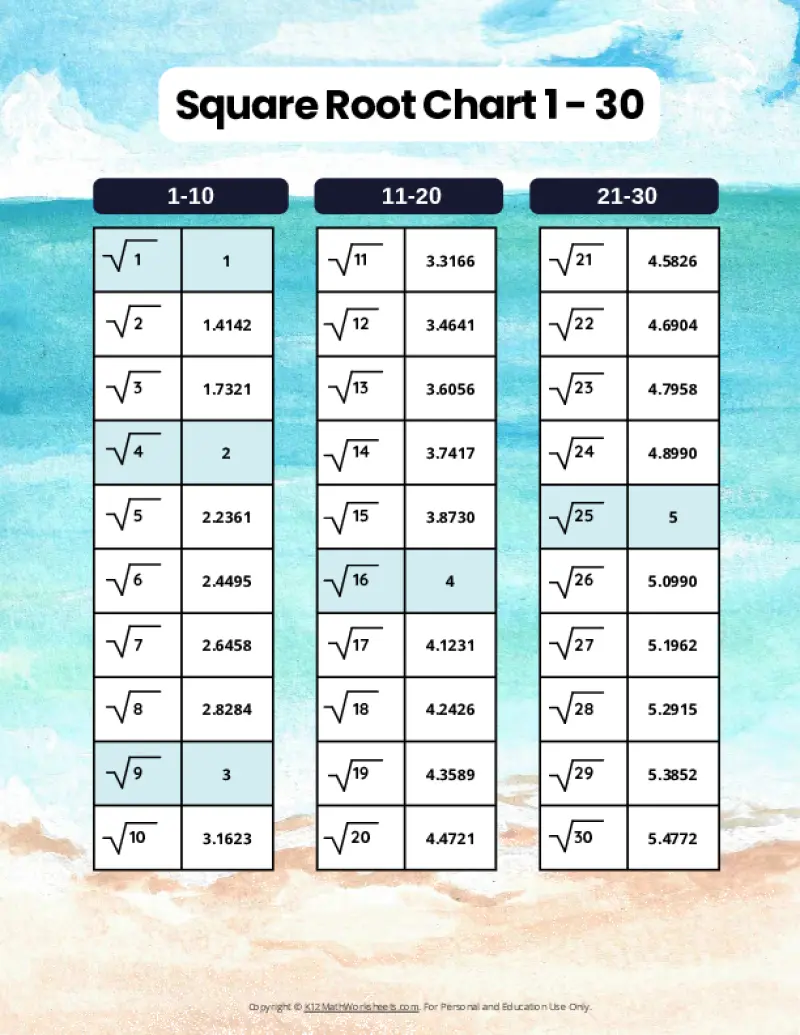
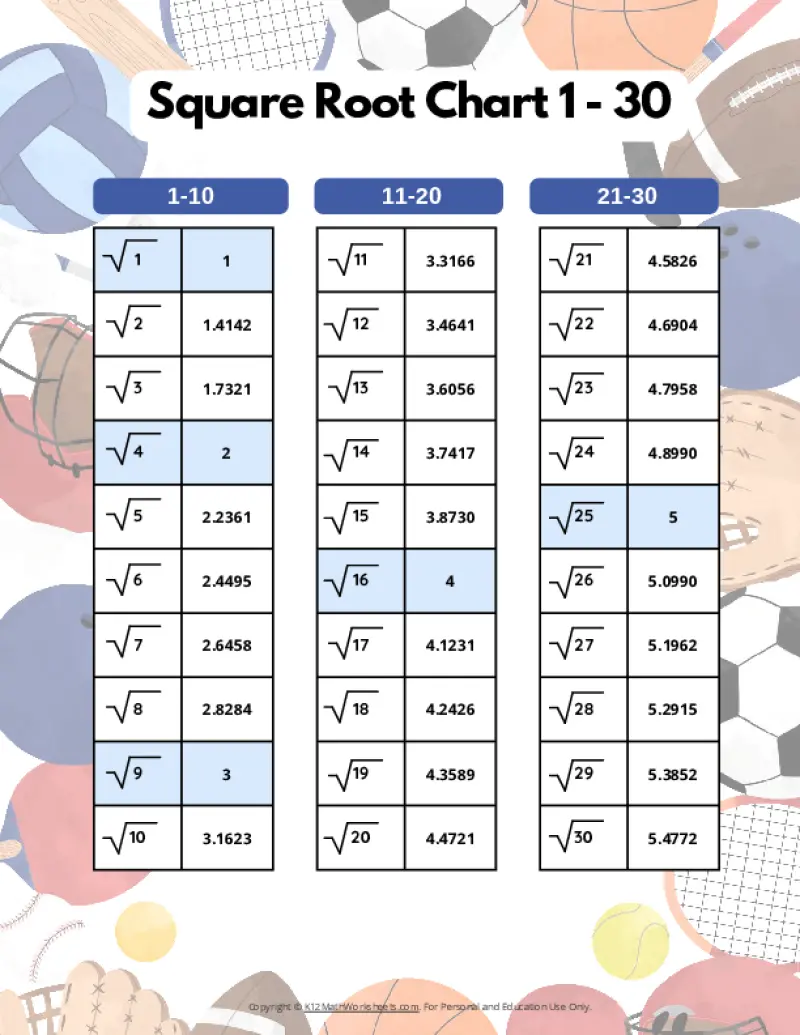
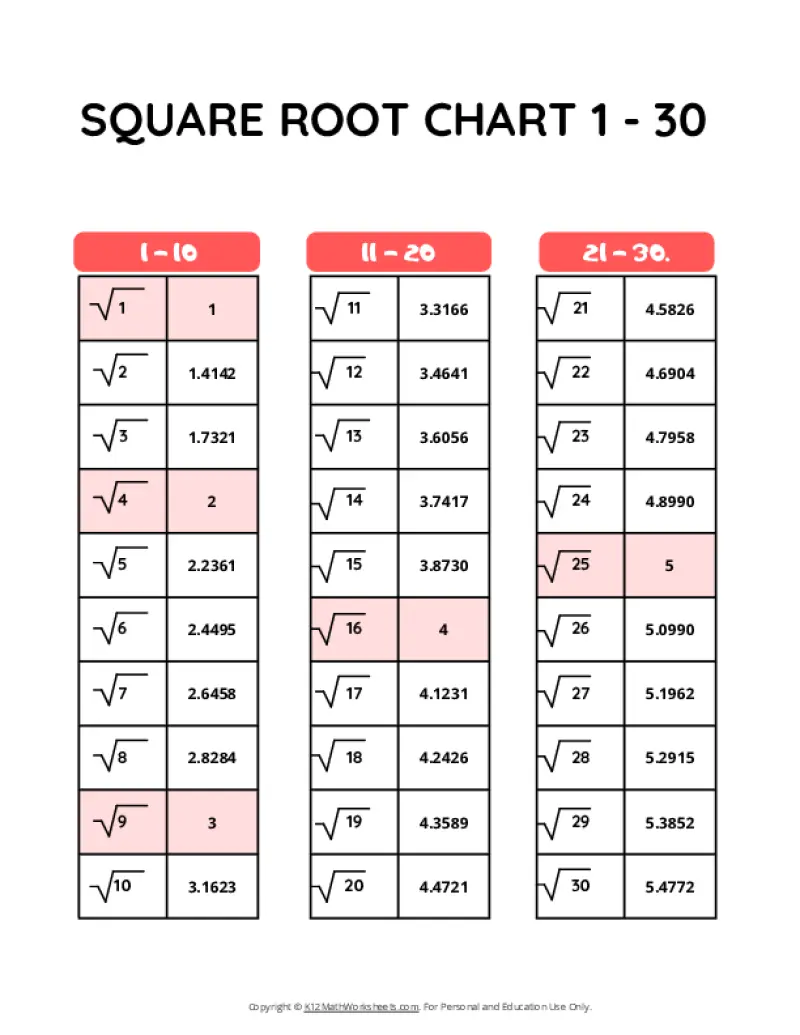
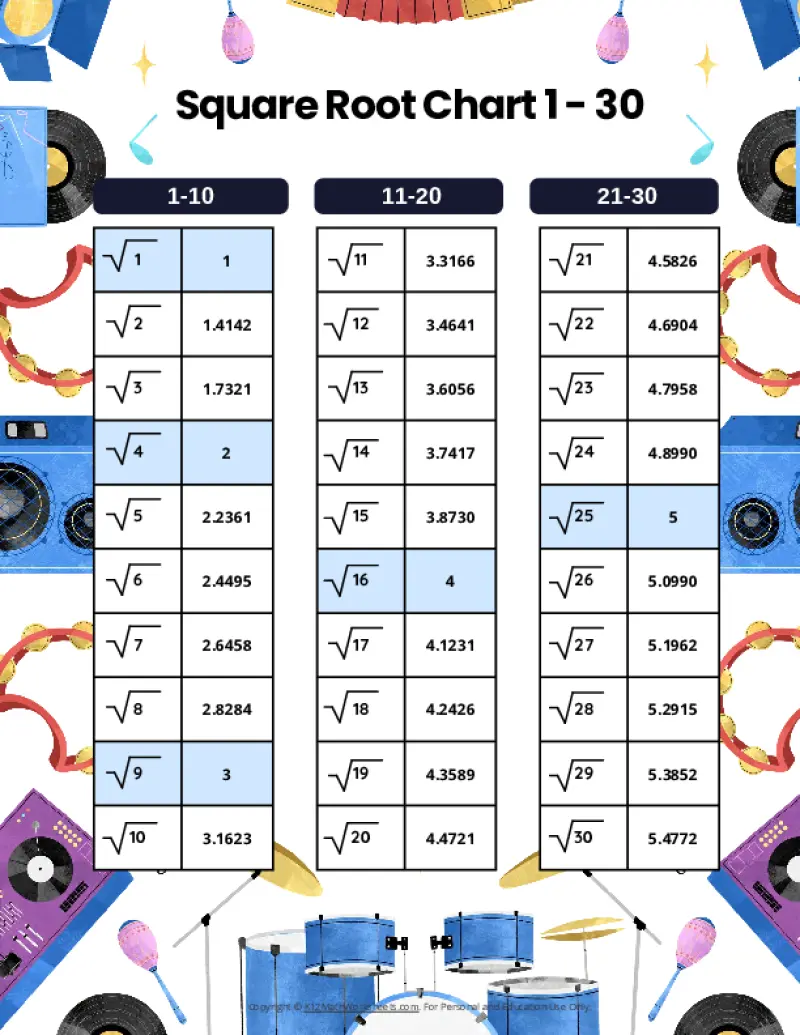
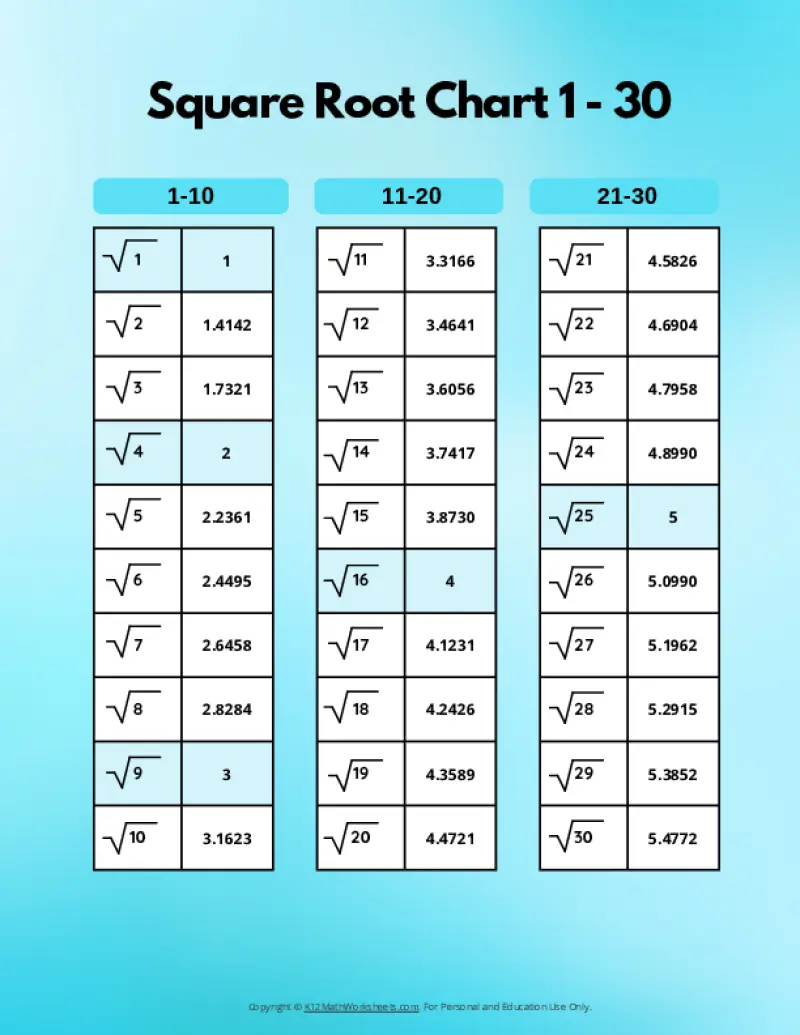
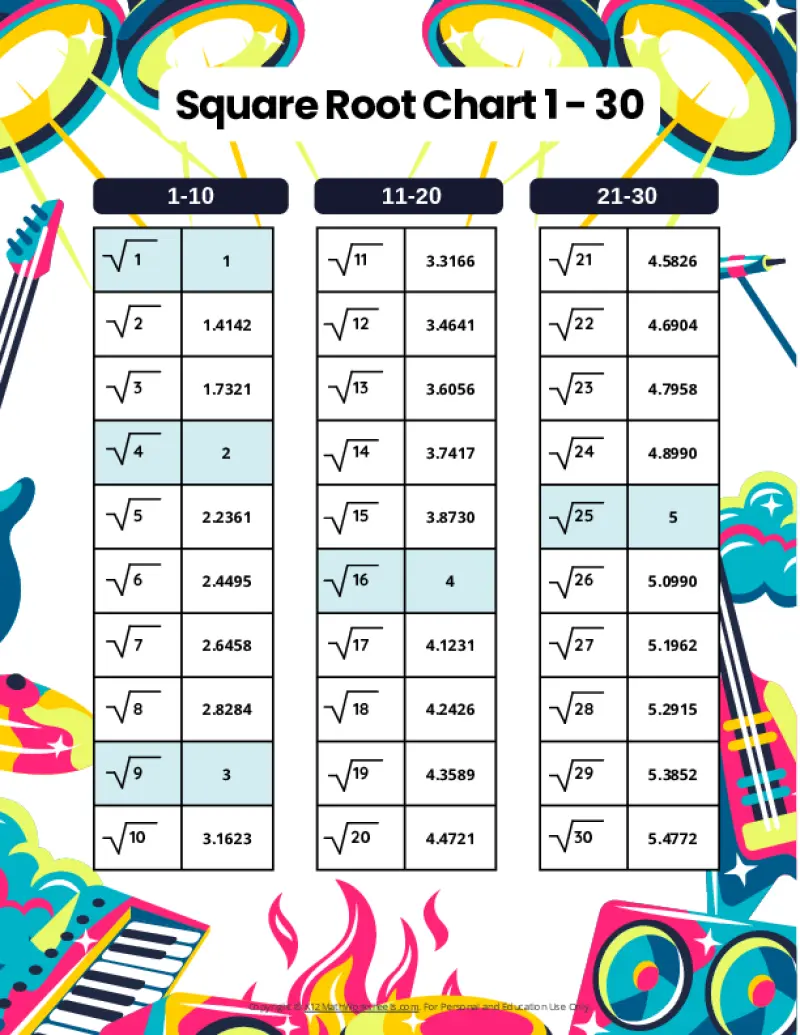
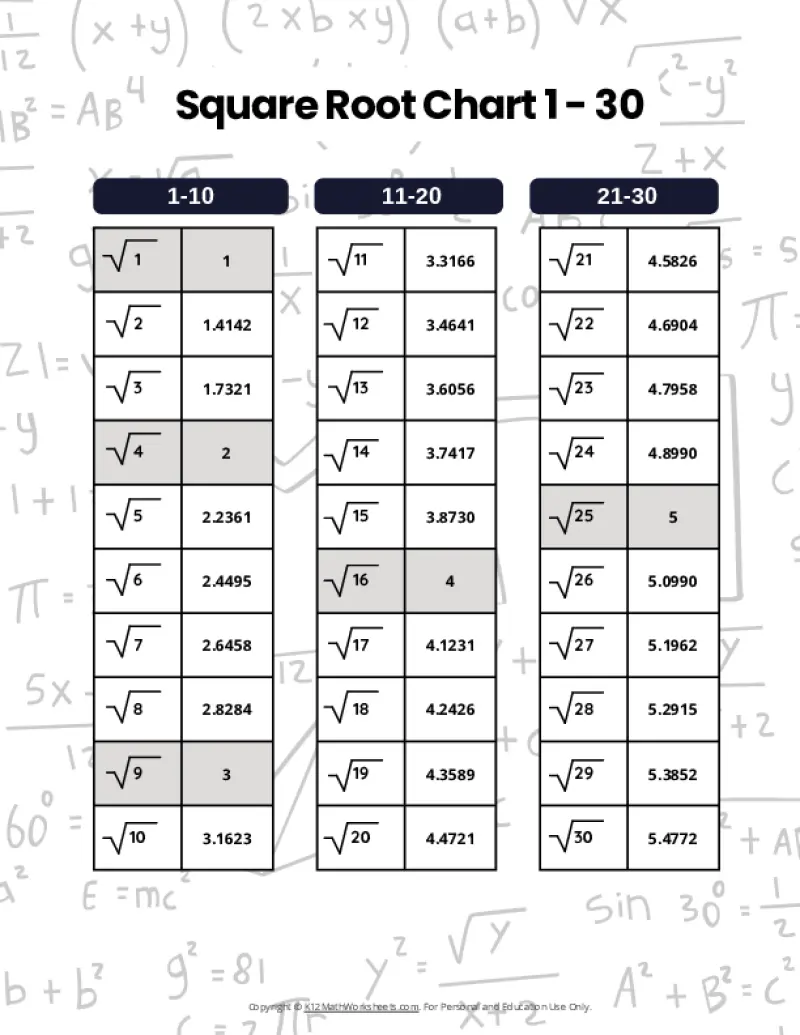
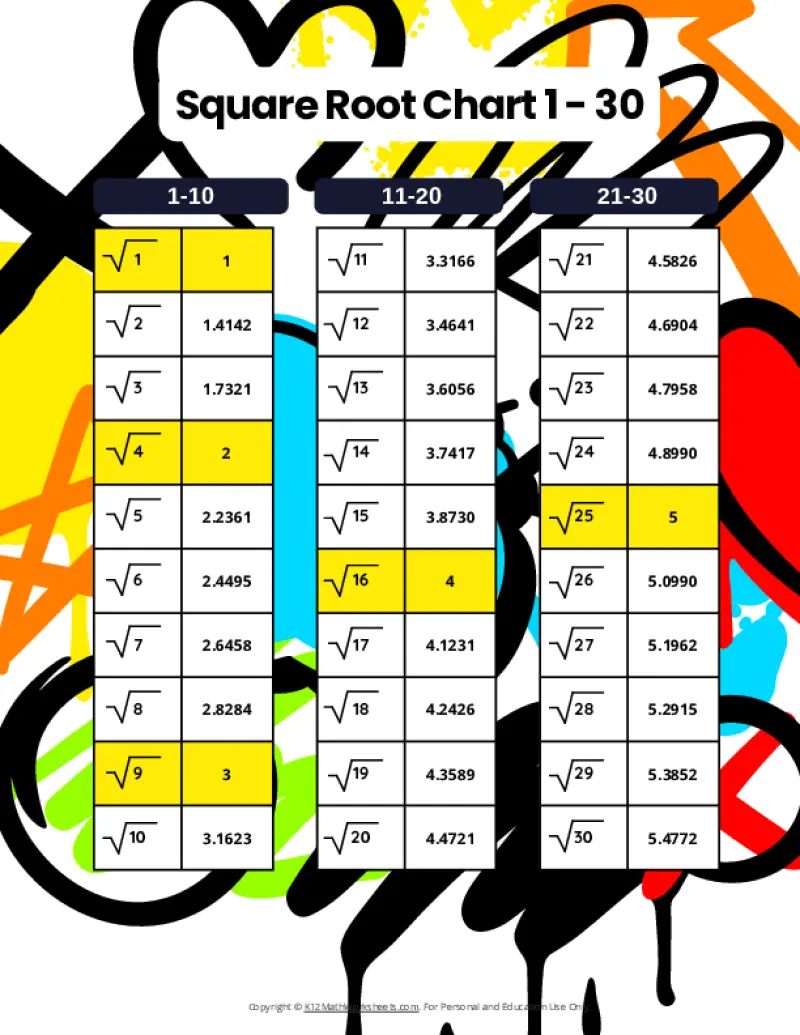
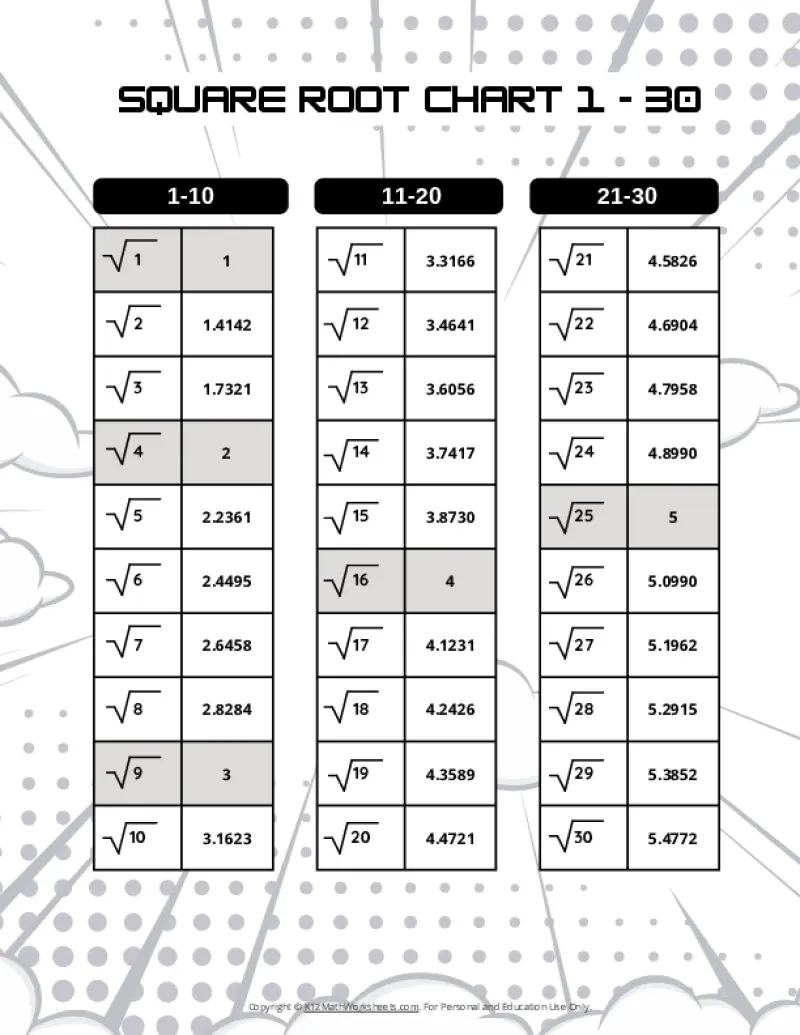
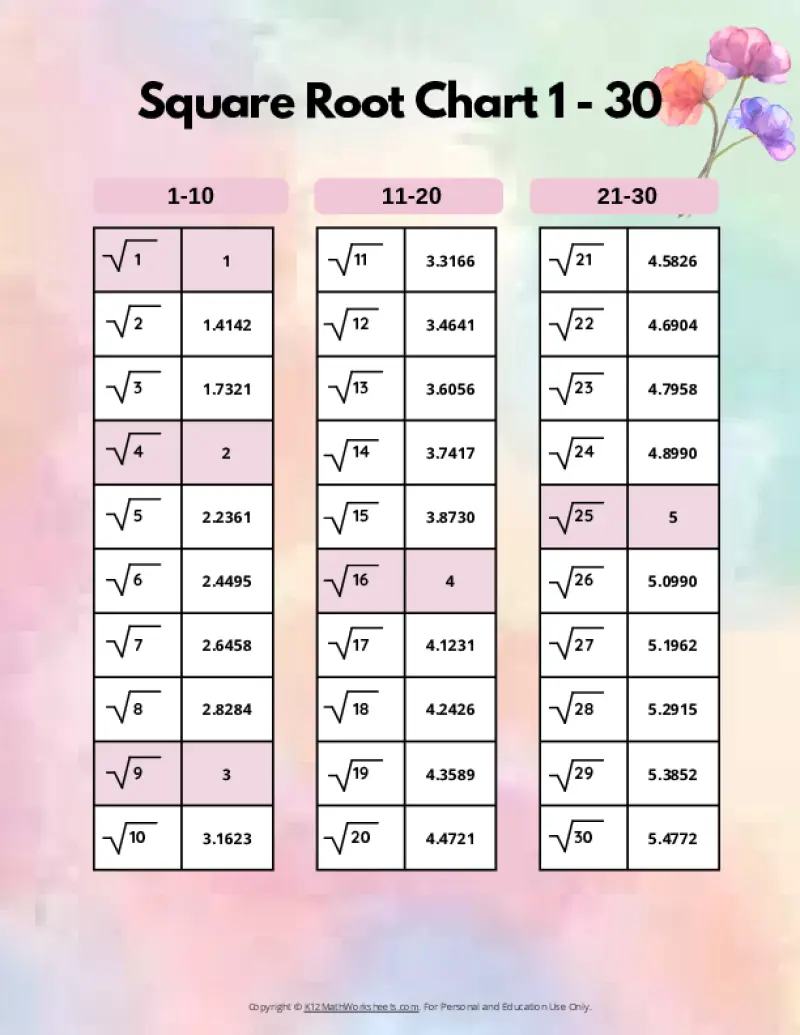
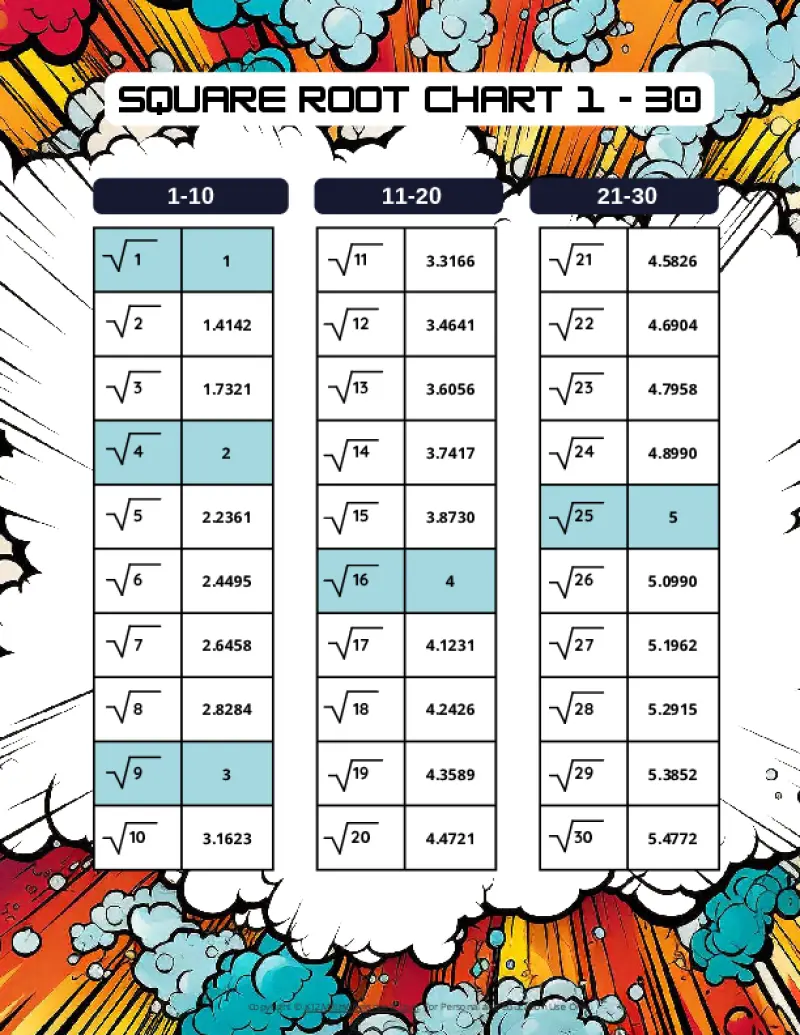
Square Root Charts for 1 to 30
Below you’ll find our selection of printable square root charts for numbers 1 through 30.
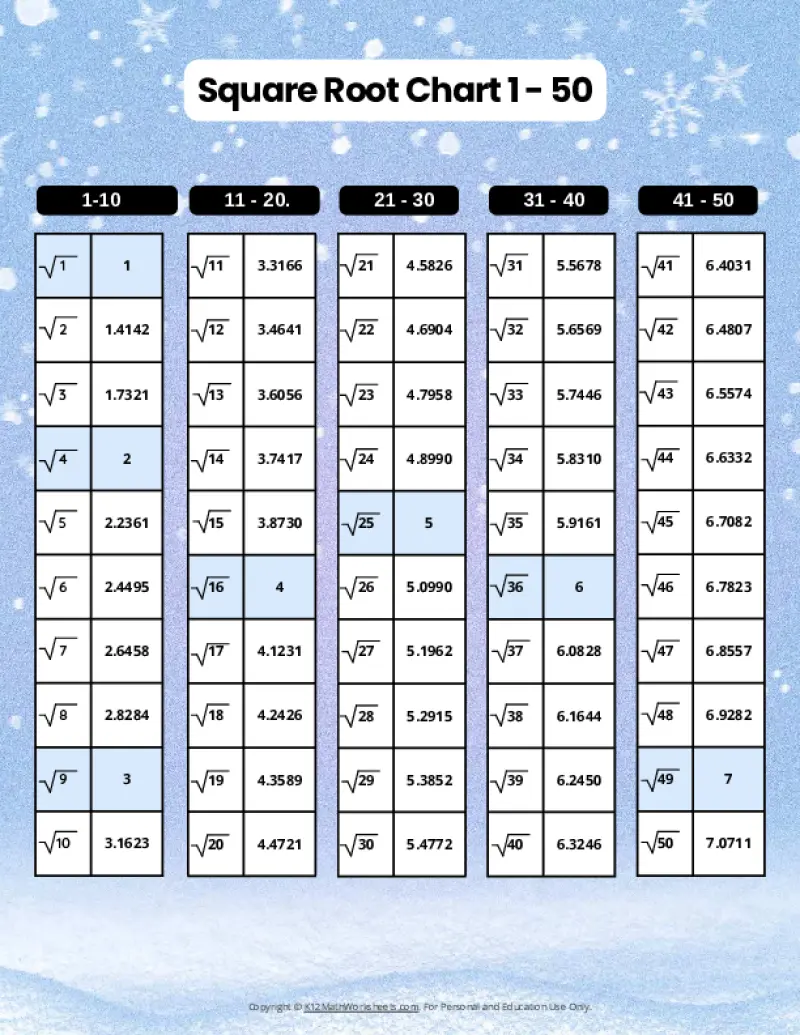
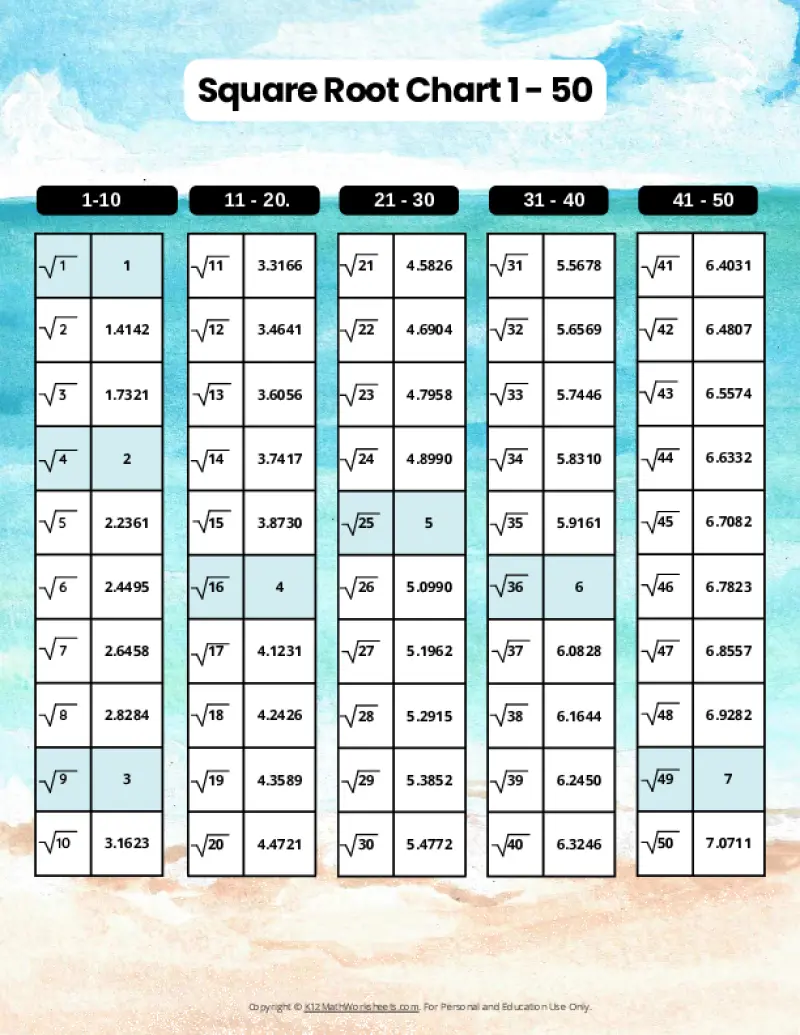
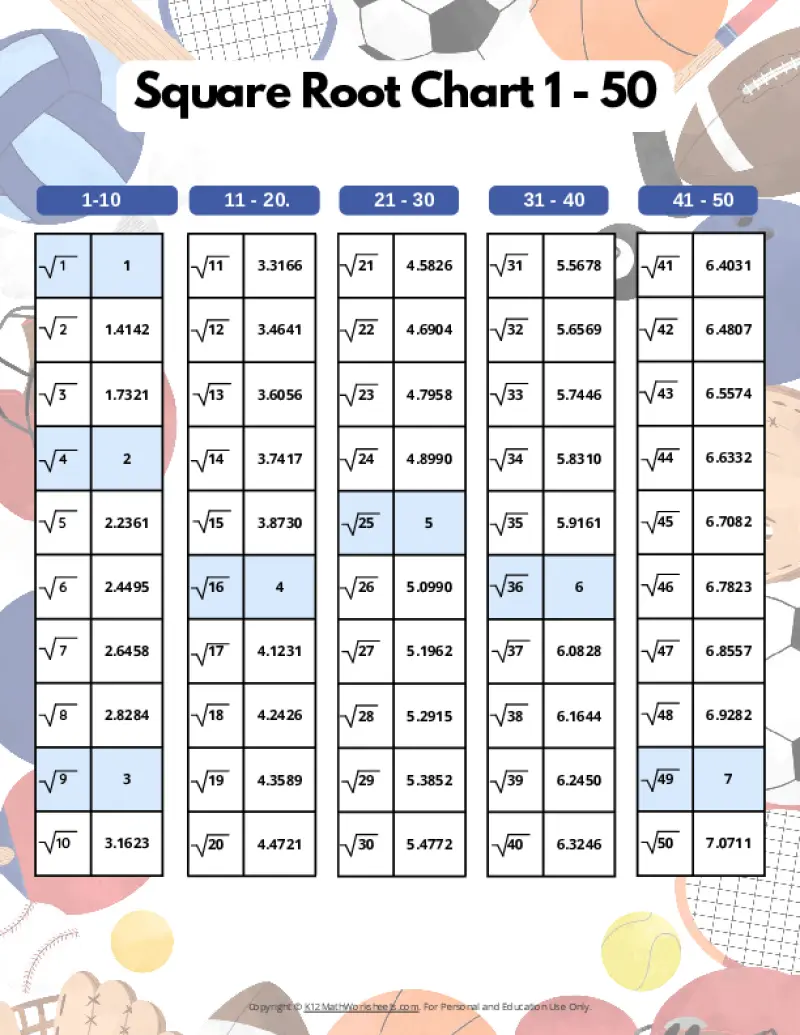
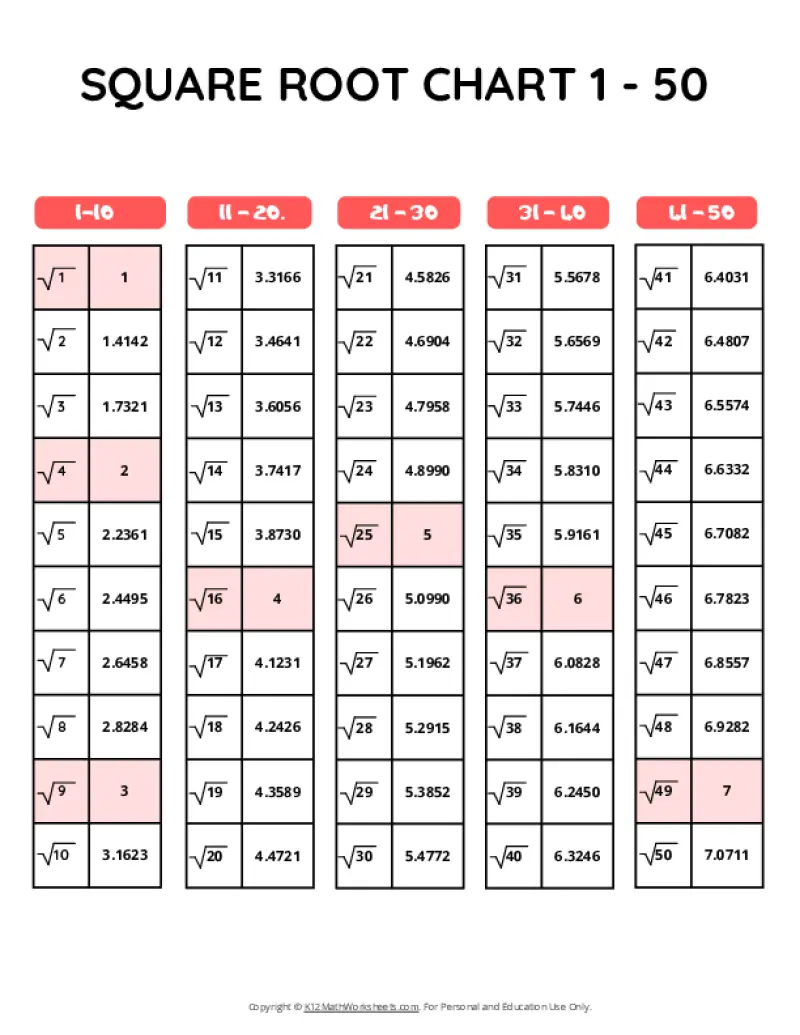
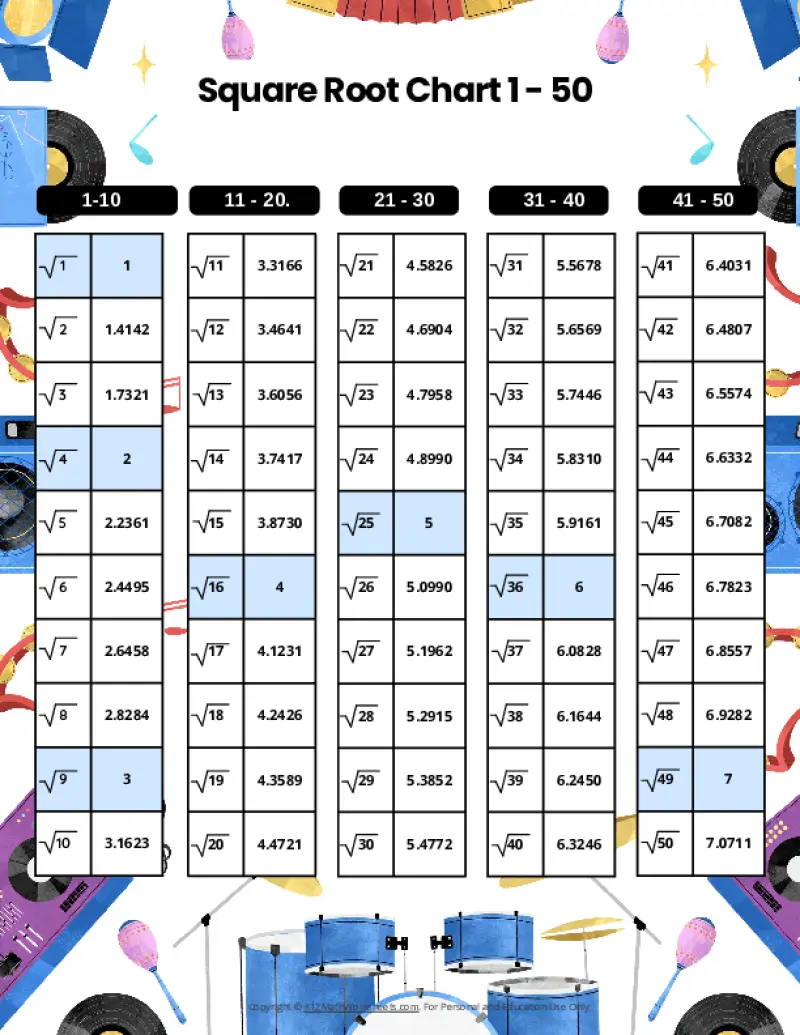
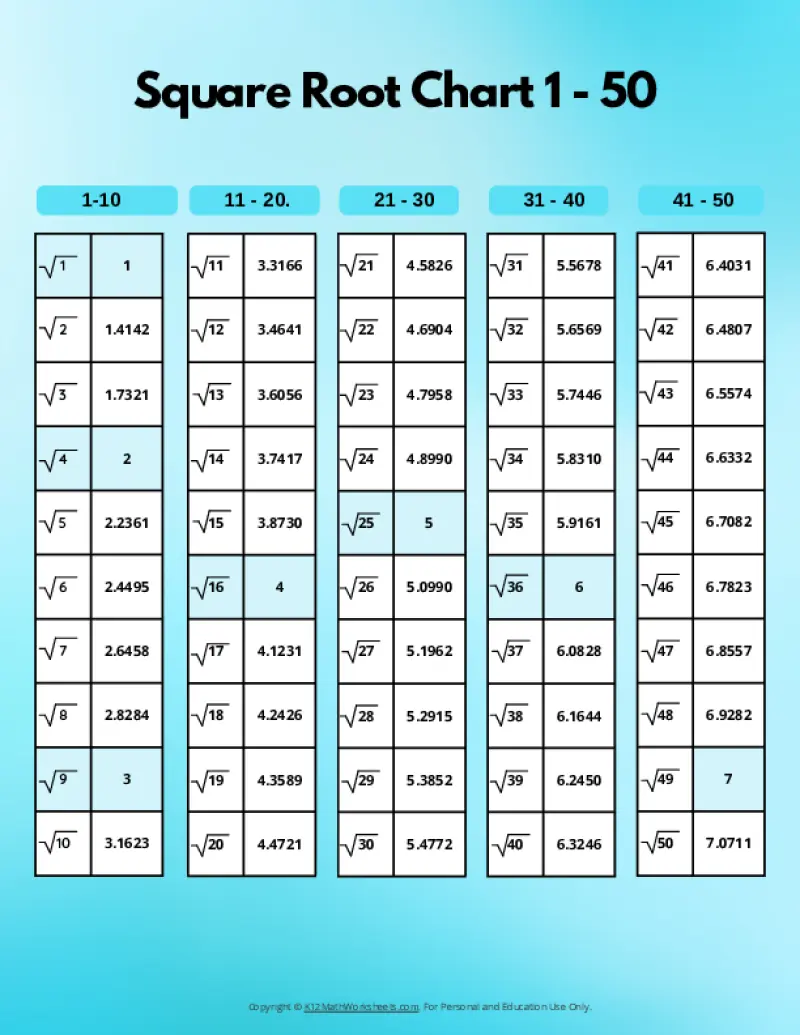
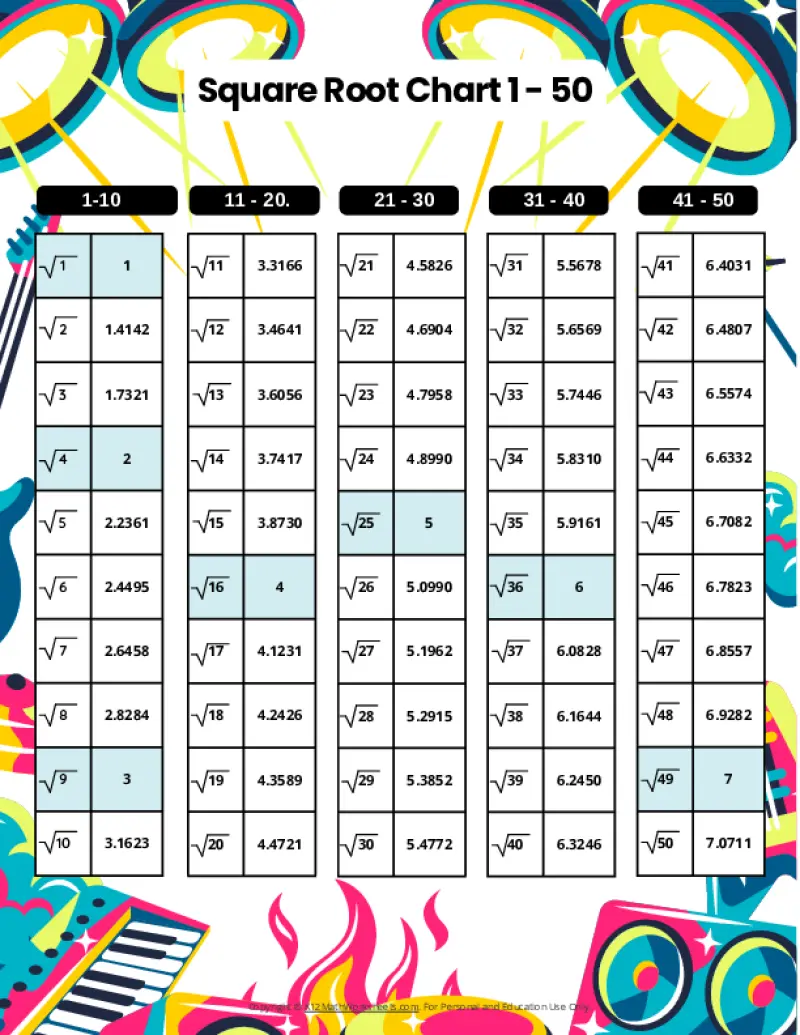
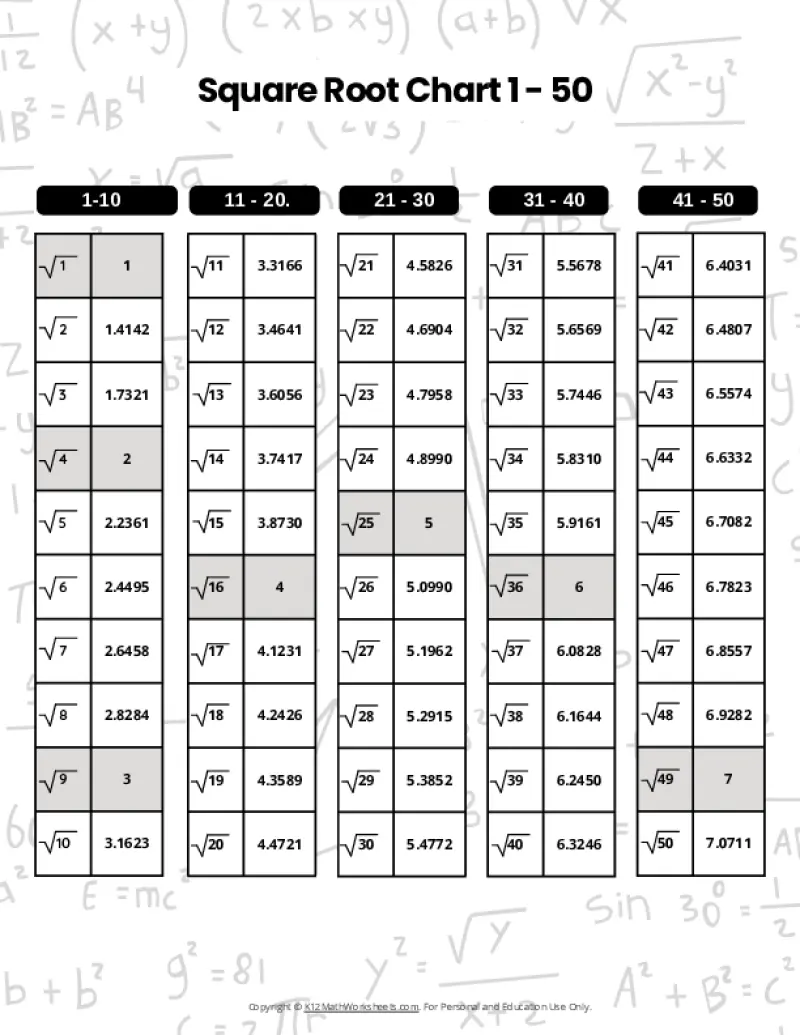
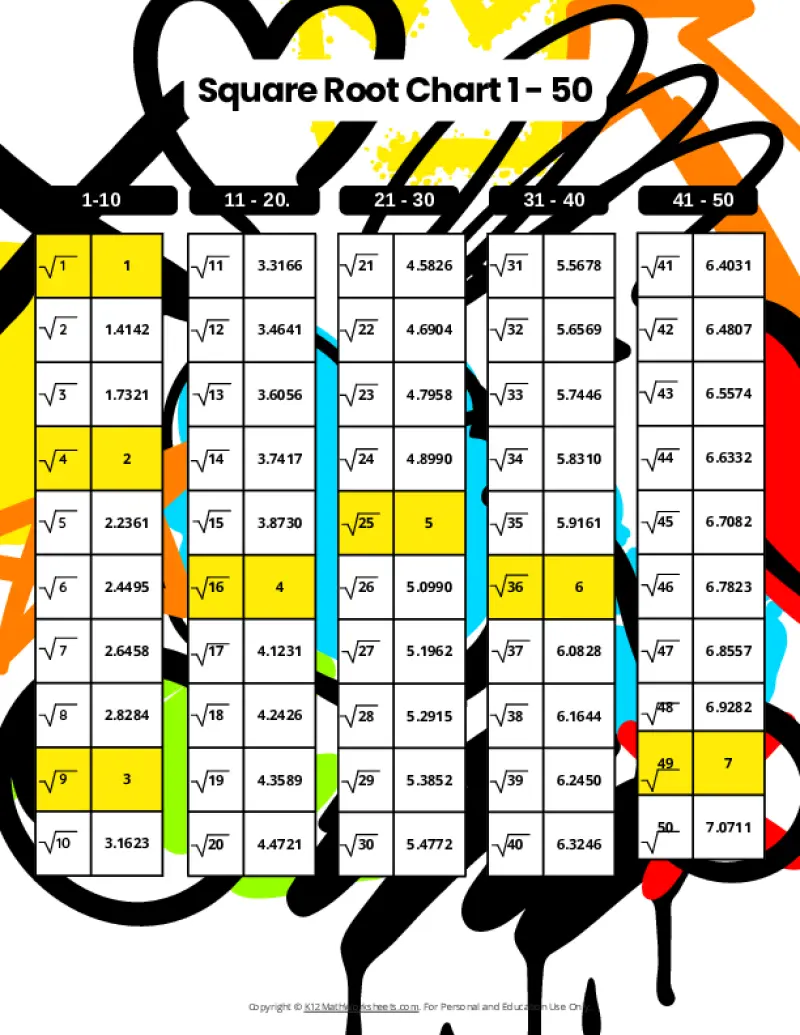
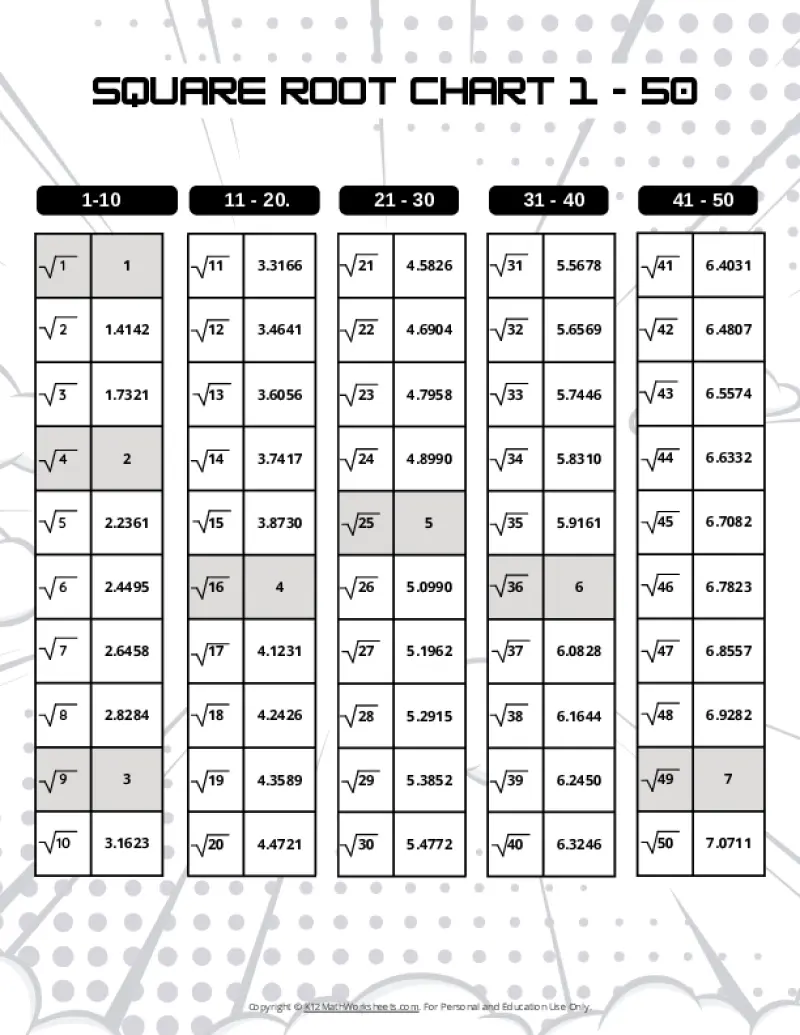
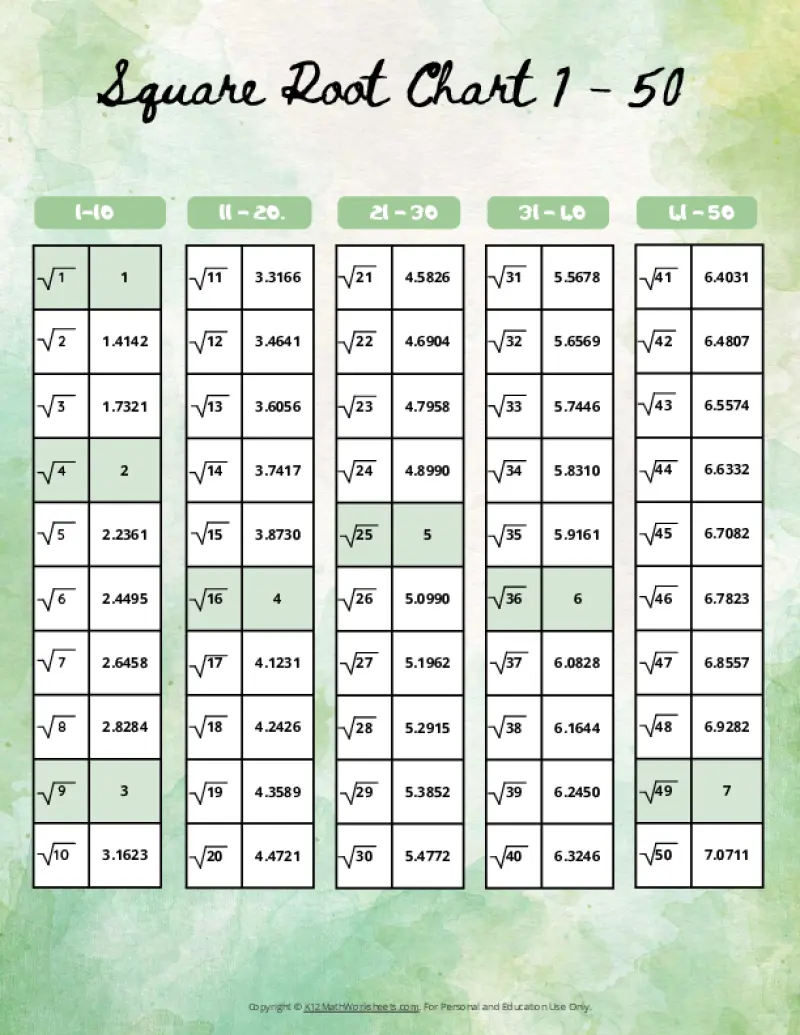
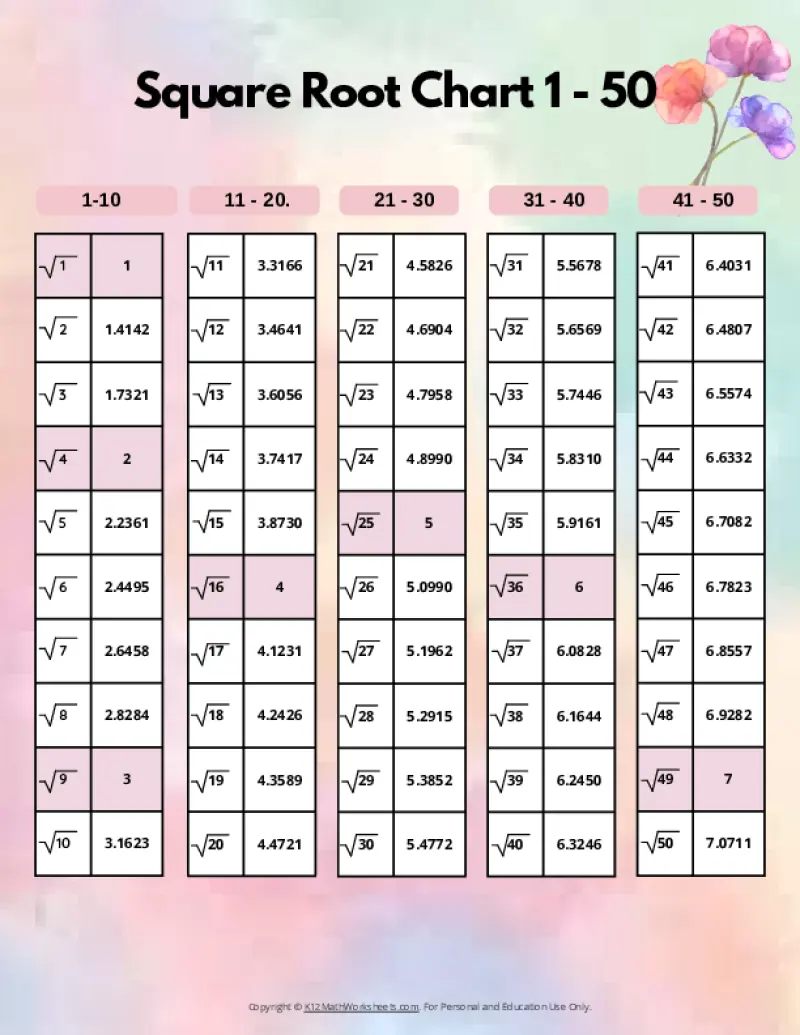
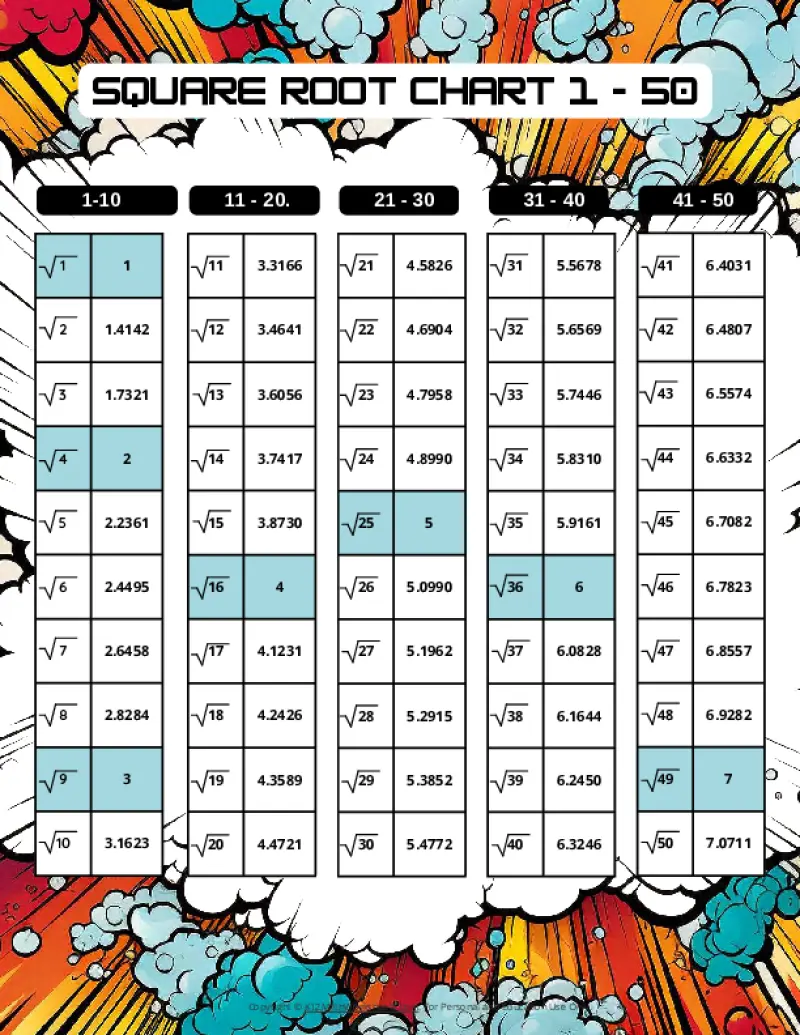
Printable PDF Square Root Charts for 1 to 50
As students progress in math, they’ll encounter square roots beyond the initial 1-30 range. Here are our printable charts covering square roots 1 through 50, perfect for middle school and beyond.
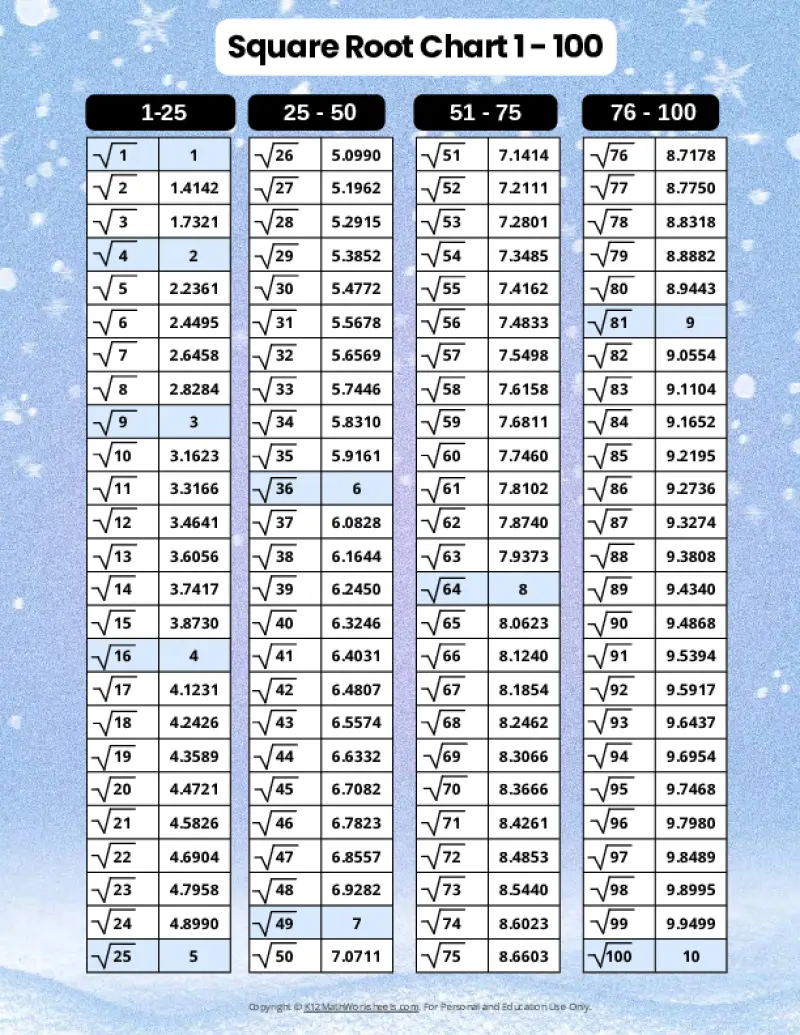
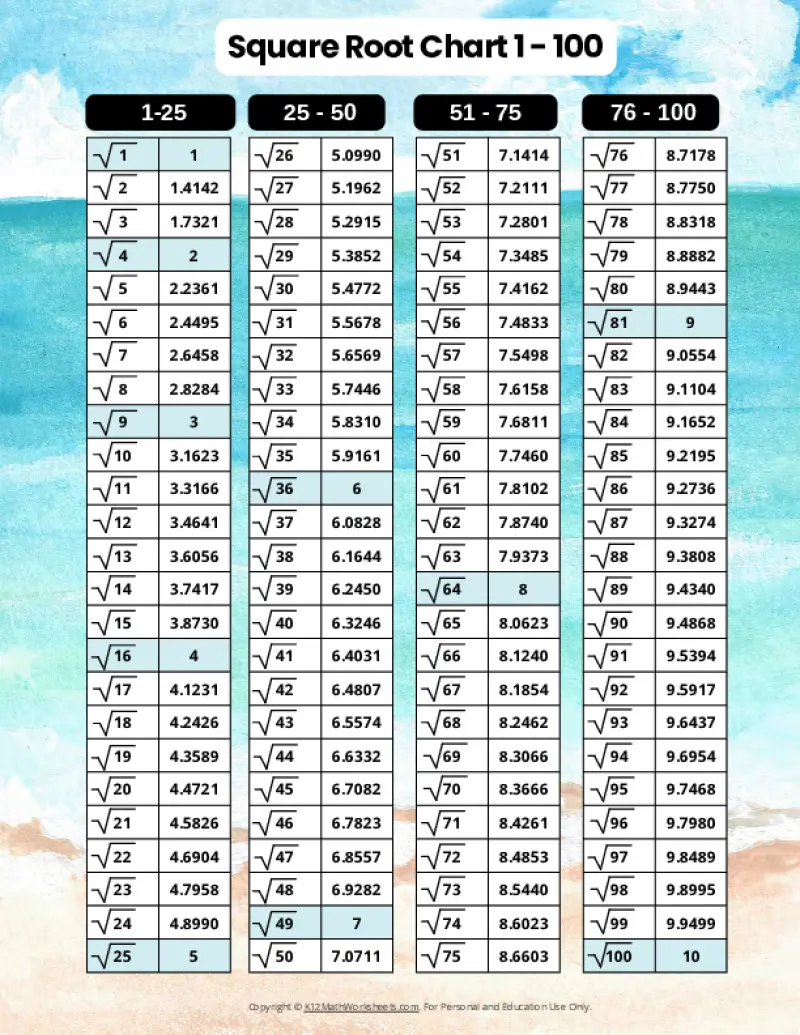
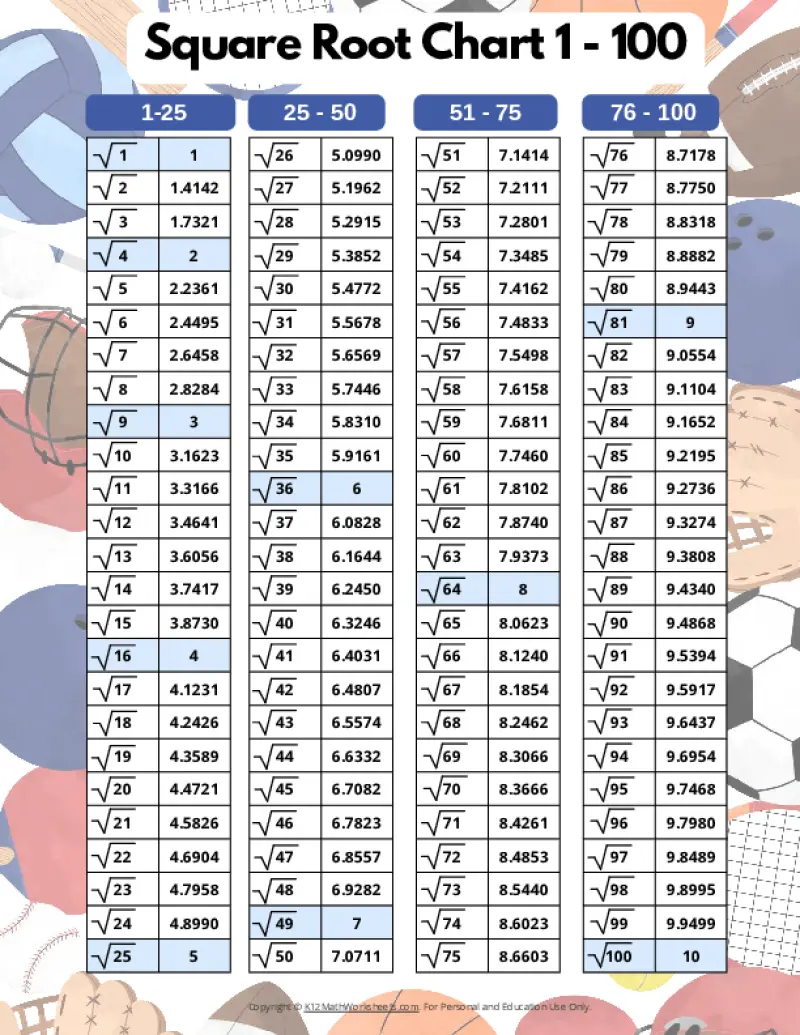
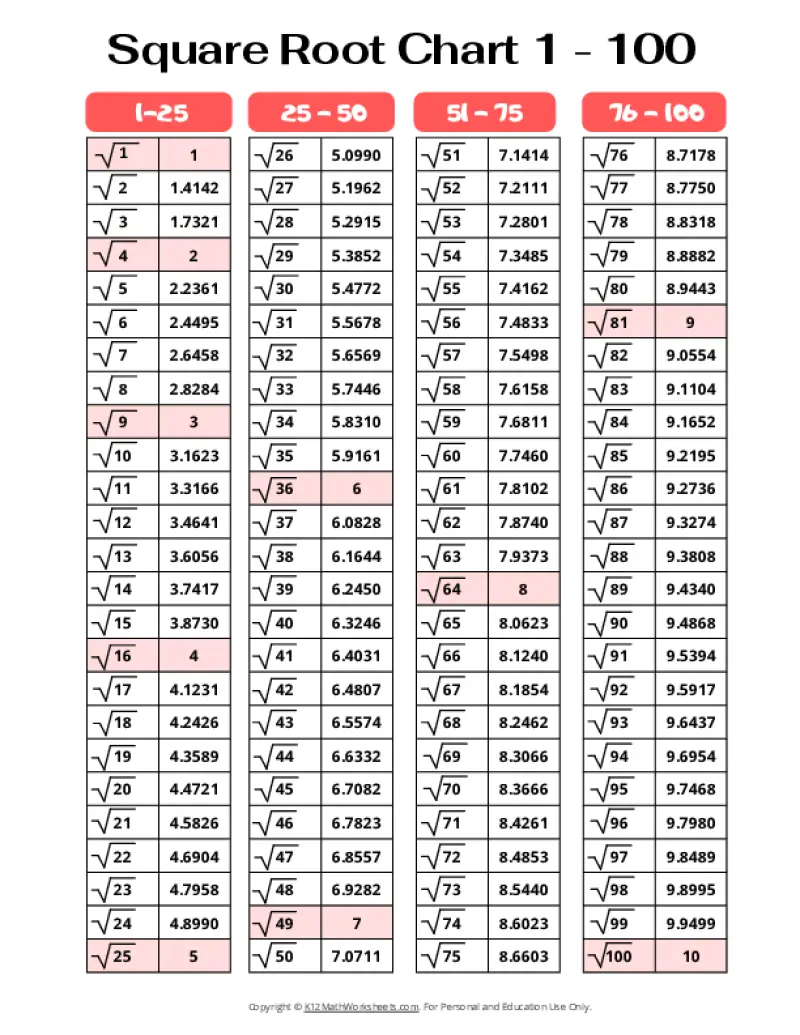
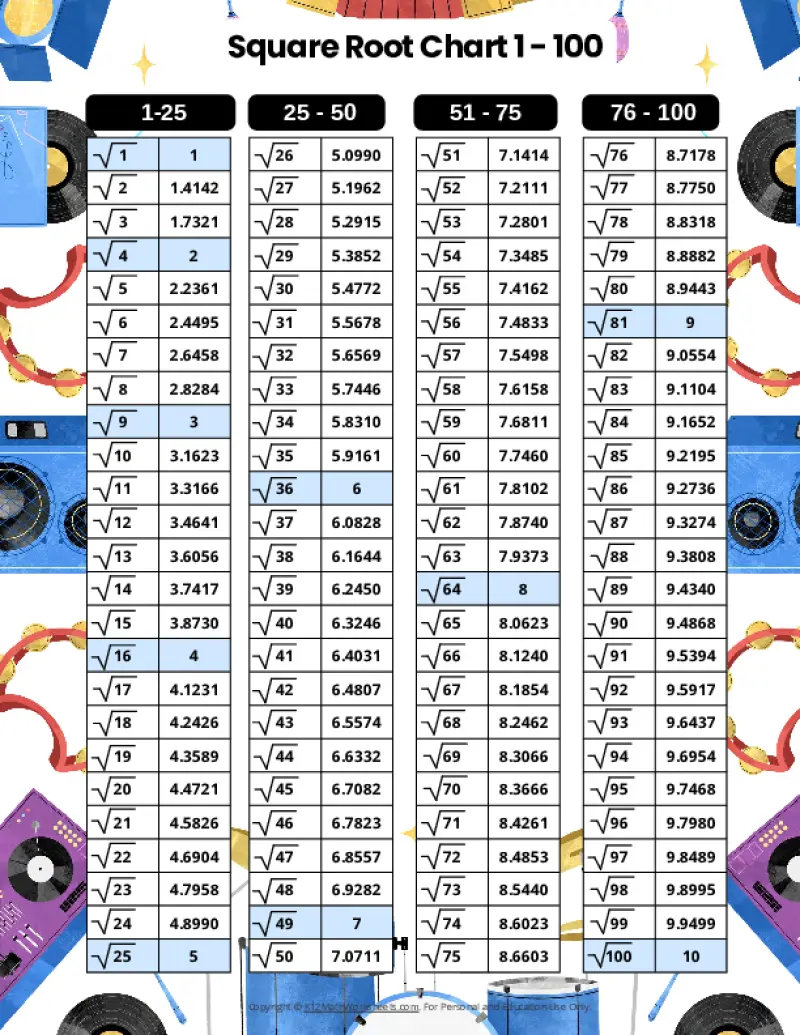
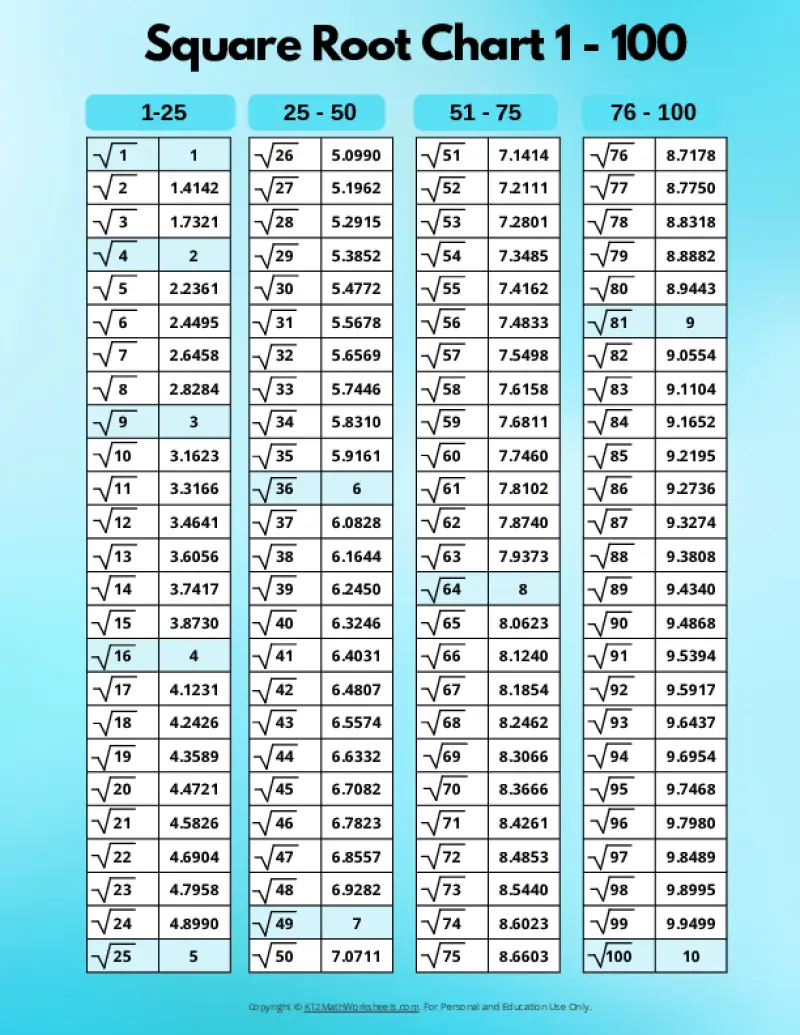
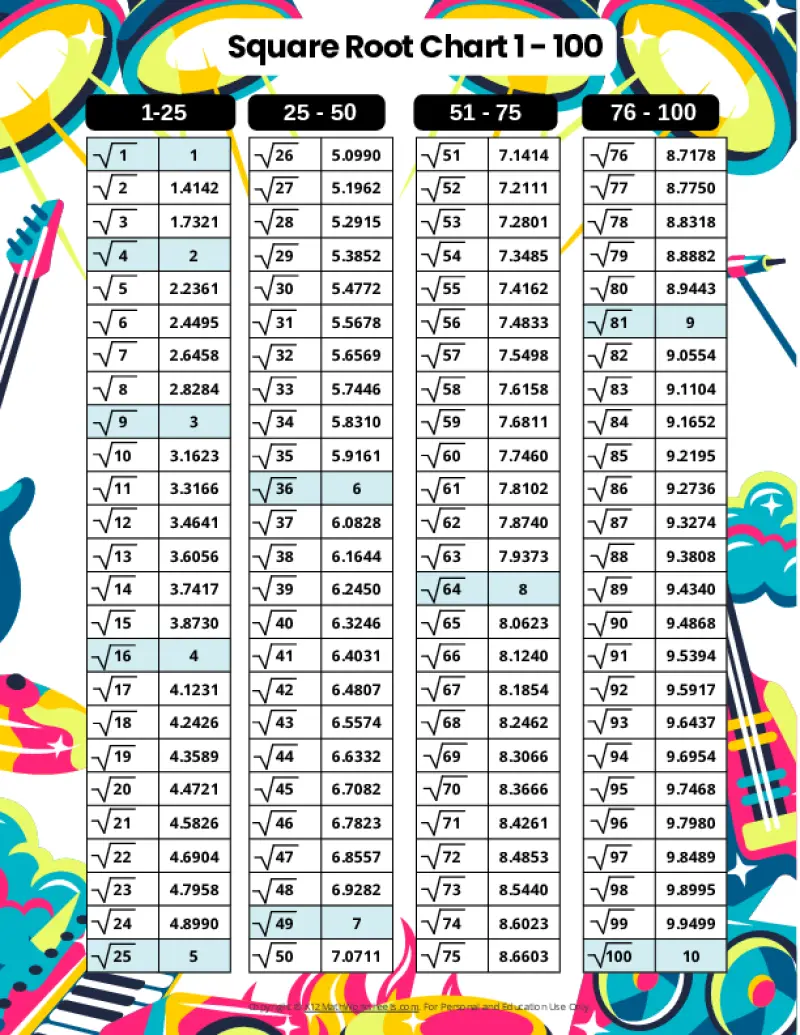
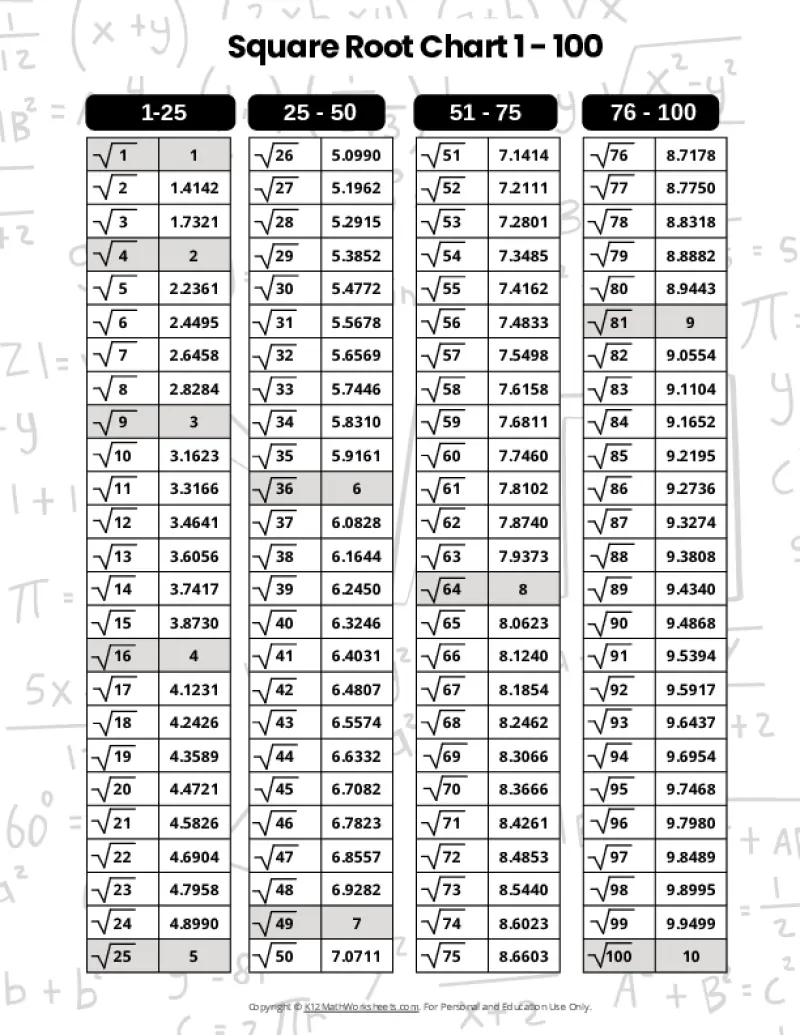
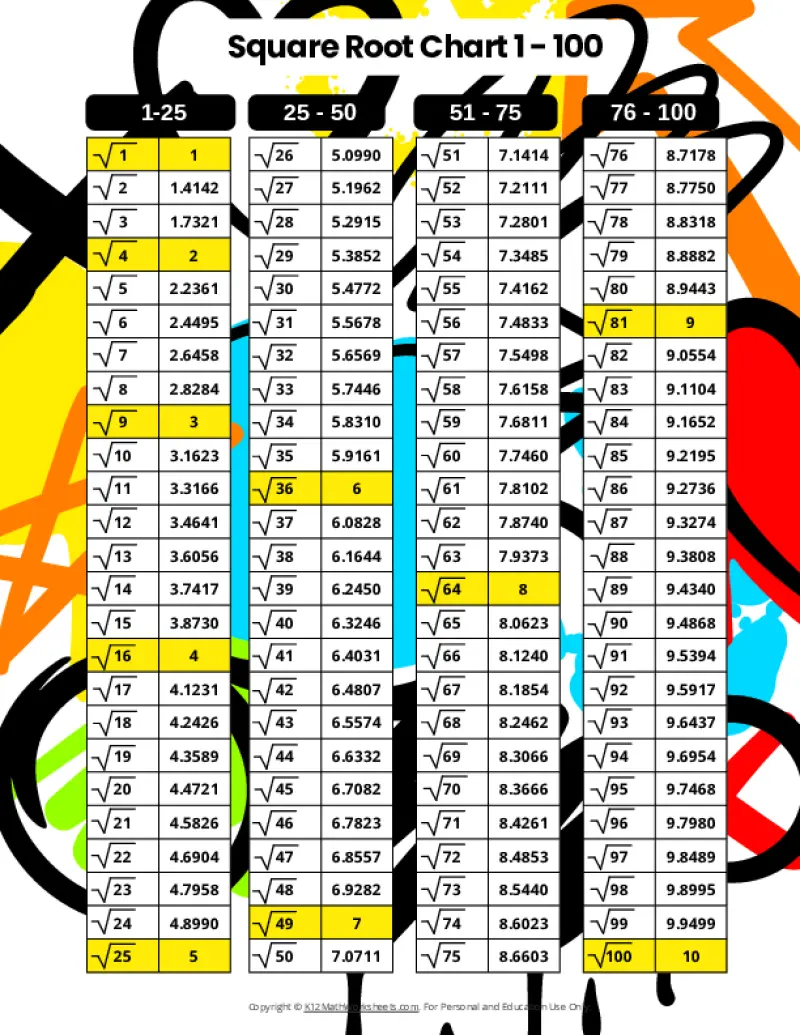
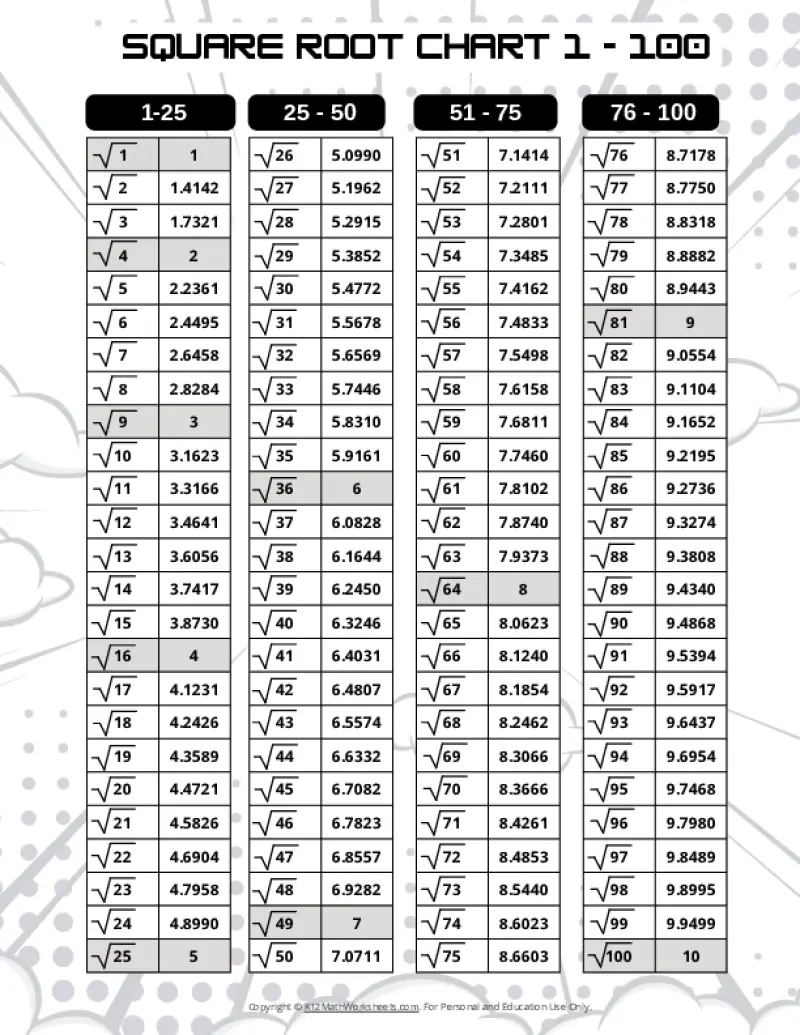
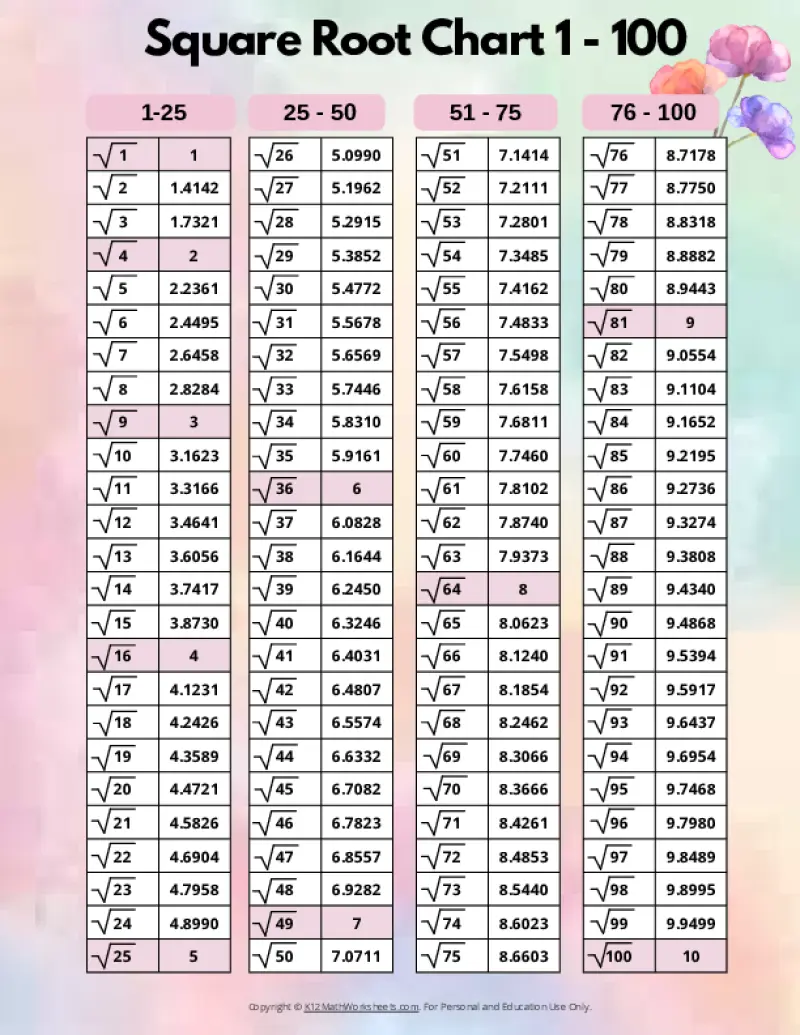
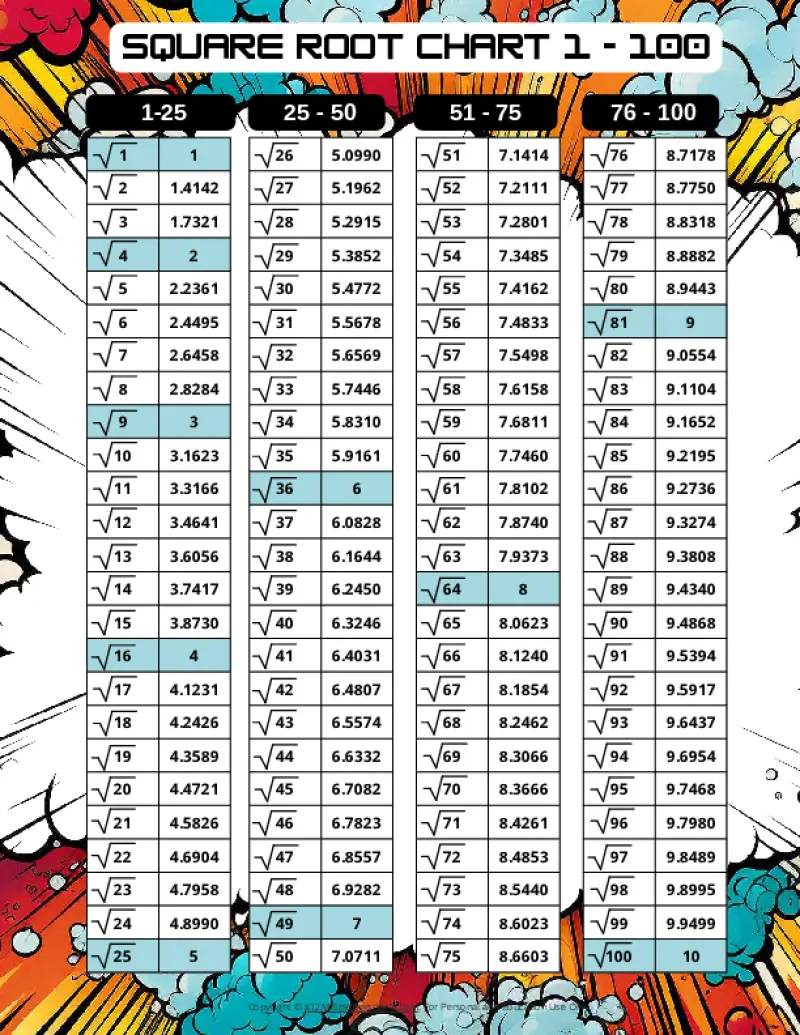
Printable PDF Square Root Charts for 1 to 100
From middle school math to advanced algebra, understanding square roots up to 100 is essential. These printable charts, offered in a variety of designed themes, provide a valuable resource for students of all levels. Explore the available themes below.
Understanding Square Roots: A Guide for Students and Educators
This page provides printable square root charts in a variety of engaging themes and ranges, designed to support students in mastering this fundamental math concept. We offer charts for square roots 1-30 (ideal for elementary and early middle school), 1-50 (commonly used in middle school), and 1-100 (a valuable resource for middle school, high school, and beyond). But what exactly are square roots, and why are they so important?
What are Square Roots?
At its core, a square root is the inverse operation of squaring a number. Think of it like this: if squaring a number means multiplying it by itself (e.g., 5 * 5 = 25), then finding the square root means asking, “What number, when multiplied by itself, equals this number?” (e.g., the square root of 25 is 5). Students are often familiar with other inverse operations, like addition and subtraction, which can be a helpful analogy.
More formally, the square root of a number (a) is another number (b) that, when multiplied by itself, equals (a). This can be represented as b * b = a. For example, 4 * 4 = 16, so 4 is the square root of 16.
Perfect Squares vs. Imperfect Squares
When a number is the product of an integer multiplied by itself (like 16 above), it’s called a perfect square. The square root of a perfect square is always a whole number (an integer). However, many numbers are not perfect squares (like 10, for example). The square root of such a number is an imperfect square, and it will be a decimal number that goes on forever without repeating (an irrational number). For practical purposes, these imperfect square roots are often rounded to a certain number of decimal places. The charts on this page round imperfect square roots to four decimal places.
Calculating Square Roots
Calculating square roots, especially of imperfect squares, can be complex. While calculators use sophisticated algorithms, the basic process involves estimation and refinement. You start with an educated guess and then refine that guess until you reach the desired level of accuracy. You can find more information about manual calculation methods on resources like Wikipedia.
Beyond Square Roots: Higher Order Roots
Square roots are just one type of root. There are also cube roots (where you find a number that, when multiplied by itself three times, equals a given number), fourth roots, fifth roots, and so on. For example, 2 * 2 * 2 = 8, so the cube root of 8 is 2. While higher roots exist, square roots and cube roots are the most commonly encountered.
Principal Roots and Roots of Negative Numbers
Every positive number actually has two square roots: a positive one and a negative one (because a negative number multiplied by itself also yields a positive result). For example, both 3 and -3, when squared, equal 9. The positive root is called the principal root.
What about the square roots of negative numbers? Since no real number, when multiplied by itself, can produce a negative result, the square roots of negative numbers are imaginary numbers. These involve the imaginary unit “i,” where i is defined as the square root of -1.