What are complementary angles and how do you find them?

• Complementary angles are a set of two angles whose measures add up to 90°. For example, if one angle measures 23° and another measures 67°, they are complementary because their sum is 90°.
• There are many ways to identify complementary angles.
  • Let’s assume you’re given one angle measure of 59° and asked to find its complement. You would subtract 59° from 90° to get 31°. That means the complement to 59° is 31°.
  • You may also be given a picture, like the one below, and told to identify complementary angles.

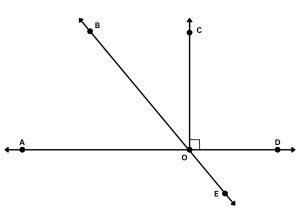
• • Remember that complementary angles are two angles whose measurements add up to 90°. Assuming that AOD is a straight line (which equals 180°), if ∠COD = 90° then ∠AOC = 90° as well. That means the two angles that make up ∠AOC are complementary angles. See below.

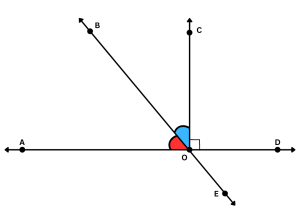
• • ∠AOB and ∠BOC are complementary angles.

What are supplementary angles and how do you find them?

• Supplementary angles are a set of two angles whose measures add up to 180°. For example, if one angle measures 123° and another measures 57°, they are complementary because their sum is 180°.
• There are many ways to identify supplementary angles.
  • If you’re given one angle measure of 159° and asked to find its supplement. You would subtract 159° from 180° to get 21°. That means the supplement to 159° is 21°.
  • You may also be given a picture, like the one below, and told to identify supplementary angles.

• • Remember that supplementary angles are two angles whose measurements add up to 180°. Assuming that AOD and BOE are both straight lines (which equal 180°), then all of the following pair of angles are supplementary:
    • ∠AOB and ∠BOD
    • ∠AOC and ∠COD
    • ∠BOC and ∠COE
    • ∠BOD and ∠DOE
    • ∠DOE and ∠EOA
    • ∠EOA and ∠AOB
  • Here is a picture of the second pair of angles from the list above, so you can see what they look like and how they add up to 180°:

What are vertical angles and how do you identify them?

• When two straight lines cross each other, four angles are created. Vertical angles are the pair of angles across from each other.

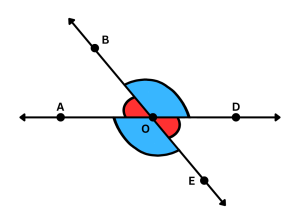
• In this image, the vertical angle pairs are:
  • ∠AOB and ∠EOD (the red angles)
  • ∠BOD and ∠AOE (the blue angles)
• The best way to identify vertical angles (given an image) is to ask yourself, “If I extend both arms of one angle, does it create both arms of another angle?” If the answer is yes, then they are vertical angles. If the answer is no, then they aren’t.

What are adjacent angles and how are they different from vertical angles?

• You may have never heard the word adjacent before, but it’s a pretty common word that’s used even outside of math. It means “nearby” or “having a common border.” When it comes to angles, adjacent angles are right next to one another. They’re angles that share a side (or leg).
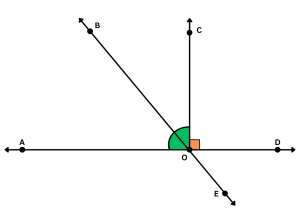
  • Remember above, when we were talking about complementary angles? The angles we identified as complementary are also adjacent. Complementary refers to their measures. Adjacent refers to their location. That’s why angles can be both complementary and adjacent. Here’s the picture so you don’t have to scroll back up to find it:

• • ∠AOB (the red angle) and ∠BOC (the blue angle) are adjacent angles because they share a common leg (side BO).
• Adjacent angles are different from vertical angles in 2 ways.
  • Their sides:
    • Adjacent angles ALWAYS share a side and are connected at the same vertex.
    • Vertical angles NEVER share a side, but they do connect at the same vertex. Remember, vertical angles are created when two straight lines cross each other. When that happens, the angles opposite each other are called vertical angles.
  • Their measures:
    • Adjacent angles MIGHT have the same measure, but it won’t always happen.
    • Vertical angles will ALWAYS have the same measure.